


Next: 函數的近似計算
Up: 數值方法
Previous: Newton 法
在高中的課本裡介紹有矩形法、梯形法和 Simpson 法等三種方法來計算間隔
[a,b] 上的連續函數 f(x) 的定積分
的近似值. 我們將 [a,b] 分成 n 等分,
令其分點為
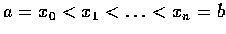 .
又令
.
又令
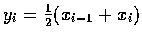 ,
h=(b-a)/n.
則 I 用各種方法計算得到的近似值如下:
,
h=(b-a)/n.
則 I 用各種方法計算得到的近似值如下:
- 左端點矩形法
-
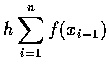 .
.
- 右端點矩形法
-
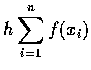 .
.
- 中端點矩形法
-
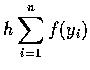 ,
我們用 R 表示這個近似值.
,
我們用 R 表示這個近似值.
- 梯形法
-
![$\displaystyle h\left[\frac{f(a)+f(b)}{2}
+\sum_{i=1}^{n-1}f(x_{i})\right]$](img186.gif) ,
我們用 T 表示這個近似值.
,
我們用 T 表示這個近似值.
- Simpson法
- (T+2R)/3.
1999-06-27
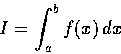
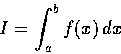
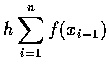 .
.
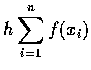 .
.
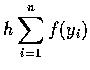 ,
我們用 R 表示這個近似值.
,
我們用 R 表示這個近似值.
![$\displaystyle h\left[\frac{f(a)+f(b)}{2}
+\sum_{i=1}^{n-1}f(x_{i})\right]$](img186.gif) ,
我們用 T 表示這個近似值.
,
我們用 T 表示這個近似值.