Next: 指數函數和對數函數
Up: 初等函數及其導函數
Previous: 多項式和有理函數
在高中時代, 先是把三角函數看成角的函數,
後來又把三角函數看成實數的函數: 設 x 為實數, A 為 x 弧度
(radian) 的角, 即單位圓上長度等於 x 的圓弧所對的圓心角,
則 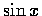 ,
,
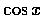 ,
,
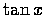 ,
,
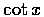 ,
,
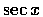 和
和 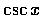 的意義分別是
的意義分別是 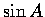 ,
,
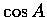 ,
,
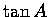 ,
,
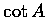 ,
,
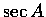 和
和 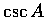 .
注意:
.
注意: 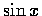 和
和 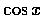 定義域都是
定義域都是
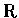 全部,
但其餘四個三角函數的定義域只是
全部,
但其餘四個三角函數的定義域只是
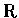 的子集合,
即
的子集合,
即 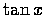 和
和 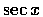 的定義域為
的定義域為
而 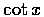 和
和 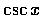 的定義域為
的定義域為
求 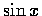 的導函數時, 我們需要不等式
的導函數時, 我們需要不等式
利用這個不等式, 可以證明
從而可得
同學們不訪回憶一下推演這個公式的手續. 有了這個公式,
其餘幾個三角函數的導函數便很容易求得了. 即
1999-06-27