積分學的均值定理

設 f(x) 為某間隔 [a,b] 的連續函數. 則

$$\frac{1}{b-a} \int_a^b{f(x)} \,dx$$

叫做 f(x) 在 [a,b] 中的均值. 積分學的均值定理是說這均值必等於 f(x) 在 [a,b] 中某一點的值. 本定理可詳述之如下:

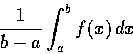
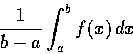
Mean-Value Theorem (one variable, integral calculus). Let f(x) be continuous on [a,b]. Then there exists a number $\varepsilon$ in [a,b] such that

$$\int_a^b{f(x)}dx=f(\varepsilon)(b-a). \eqno(1)$$

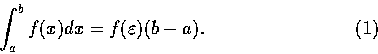
Proof. Let m and M be the minimum and maximum of f(x) on [a,b] respectively. Then $m\leq{f(x)}\leq{M}$. Integrating and dividing by b-a, we get

$$m\leq{\frac{1}{b-a}} \int_a^b{f(x)} \,dx\leq{M}.$$

Since f(x) is continuous, when x varies in [a,b], it takes on any value between m and M. Therefore there is a number $\xi \in{[a,b]}$ satisfying (1).

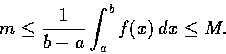
附註. 本定理結論中之 $\xi$, 可自開間隔 (a,b) 中選出--見本節後的習題 1.