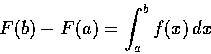
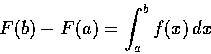
Mean-Value Theorem (1 variable,differential calculus).
Let f(x) be a continuous function on [a,b].
Assume that f'(x) exists in (a,b).
Then there exits a number
![]() such that
such that
我們先解釋一下證明的構想. 利用函數圖形,
均值定理的結論可說成: 在 f(x) 的圖形上一定有某處
![]() ,
其切線和
A=(a,f(a)) 與 B=(b,f(b) 二點的連線平行.
這結論在直觀上似乎相當明顯; 只要把 AB 向旁邊平行推移,
當移到即將離開 f 的圖形時立即停住就行了.
亦即若
,
其切線和
A=(a,f(a)) 與 B=(b,f(b) 二點的連線平行.
這結論在直觀上似乎相當明顯; 只要把 AB 向旁邊平行推移,
當移到即將離開 f 的圖形時立即停住就行了.
亦即若
![]() 是函數圖上距 AB 最遠的地方,
則此
是函數圖上距 AB 最遠的地方,
則此 ![]() 符合要求. 據此我們要研究 (x,f(x)) 到 AB 的距離.
因此從點 (
x0,y0) 到直線
符合要求. 據此我們要研究 (x,f(x)) 到 AB 的距離.
因此從點 (
x0,y0) 到直線
![]() 的距離為
的距離為
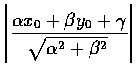 ,
故若 y=L(x) 是 AB 連線的方程式,
則
,
故若 y=L(x) 是 AB 連線的方程式,
則
![]() 和 (x,f(x)) 到直線 AB 的距離成正比.
因此只須找
和 (x,f(x)) 到直線 AB 的距離成正比.
因此只須找
![]() 的最大值所在即可. 去掉絕對值符號, 那麼
的最大值所在即可. 去掉絕對值符號, 那麼
![]() 取的最大值或最小值的地方就是符合條件的
取的最大值或最小值的地方就是符合條件的 ![]() .
.
以下我們把上面的想法寫成完整的證明:
證明. 對
![]() 定義
定義
本定理的一個特例是
Roll's Theorem. Let f(x) be a continuous fuction on [a,b].
Assume that f'(x) exists in (a,b). If f(a)=f(b),
then there exists a number ![]() in (a,b) such that
in (a,b) such that ![]() .
.
很多高中數學中用過而未證明的結果可以由均值定理推出.茲舉二例如下:
系一. 若 f'(x) 在一間隔中到處為 0, 則 f(x) 在此間隔中為一常數.
系二. 若 f'(x) 在一間隔中到處
![]() ,
則 f(x) 在此間隔中為一增函數 (嚴格增函數);
若 f'(x) 在一間隔中到處
,
則 f(x) 在此間隔中為一增函數 (嚴格增函數);
若 f'(x) 在一間隔中到處
![]() ,
則 f(x) 在此間隔中為一減函數 (嚴格減函數).
,
則 f(x) 在此間隔中為一減函數 (嚴格減函數).