


Next: 反函數
Up: 高中單變數微積分的補充
Previous: 高中單變數微積分的補充
高中微積分只講單變數函數的微積分, 但也沒有把這部份講完.
在本章和下章中我們把這些補足. 除了下章集中講積分的技巧外,
所有其餘的題材都集中在本章之中.
首先, 我們先引入一些新的函數. 和三角函數類似的, 有六個函數,
稱為 hyperbolic function (雙曲函數), 其中兩個叫做 hyperbolic sine 和 hyperbolic cosine,
定義如下:
其餘的 hyperbolic tangent, hyperbolic cotangent, hyperbolic secant, hyperbolic cosecant,
可由這兩個函數如下定義出來:
在以下的討論中, 我們以 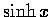 和
和 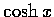 為重點.
經過簡單的計算可得
為重點.
經過簡單的計算可得
因
將二式相加減後用 2 除, 乃得以下的兩個加法公式:
這兩個公式和三角函數的加法公式相當, 在公式(1)中以 y=-x 代入, 乃得
在公式(1)和(2)中以 y=x 代入, 乃得
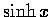 和
和 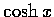 的導函數可直接以定義推出, 即
的導函數可直接以定義推出, 即
以下說明 hyperbolic functions 命名的由來:
設 t>0. 則
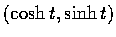 落在第一象限中雙曲線
落在第一象限中雙曲線
x2-y2=1
的一枝上. 在 (1,0) 和
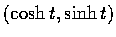 間雙曲線段和 x 軸所夾的面積為
間雙曲線段和 x 軸所夾的面積為
在這積分中以 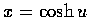 代入, 乃得
代入, 乃得
我們想像一動點自 (1,0) 沿雙曲線移動至
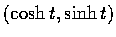 處,
則原點和該動點連線所掃過的面積是
處,
則原點和該動點連線所掃過的面積是
換言之, 在此雙曲線上取一點 (x, y). 若一動點自 (1. 0) 至此點沿雙曲線移動. 若原
點和該動點連結成的線段所掃過的面積的 2 倍為t, 則有
我們知道三角函數的別名叫做圓函數 (circular function). 所以有這個別名, 是因
為在單位圓周上取一點 (x, y) 時,
若 (1, 0) 和 (x, y) 間的圓弧和原點所張的扇形的面積的 2 倍為 t,
則 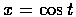 ,
,
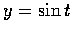 .
上述結果和這事實十分相似; 因此乃有 hyperbolic functions 之名稱.
.
上述結果和這事實十分相似; 因此乃有 hyperbolic functions 之名稱.



Next: 反函數
Up: 高中單變數微積分的補充
Previous: 高中單變數微積分的補充
1999-06-27
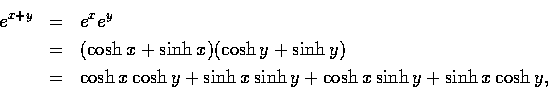

![]() 和
和 ![]() 的導函數可直接以定義推出, 即
的導函數可直接以定義推出, 即
![]() 落在第一象限中雙曲線
落在第一象限中雙曲線
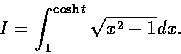
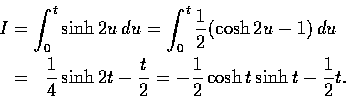
![]() 處,
則原點和該動點連線所掃過的面積是
處,
則原點和該動點連線所掃過的面積是