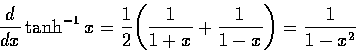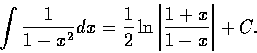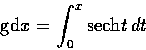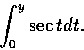Next: 均值定理
Up: 高中單變數微積分的補充
Previous: 有關反三角函數的一些積分公式
我們討論過六個 hyperbolic functions, 其中 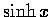 ,
,
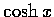 和
和 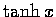 的反函數將有用處,
所以有需要給予適當的考慮.
的反函數將有用處,
所以有需要給予適當的考慮.
A. 因為 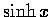 的導函數
的導函數 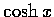 到處為正,
所以它是一個狹義增函數. 不須縮減它的定義域便可定義其反函數.
這時的問題便是給定 x 要解 y 的方程式
到處為正,
所以它是一個狹義增函數. 不須縮減它的定義域便可定義其反函數.
這時的問題便是給定 x 要解 y 的方程式
則
e2y-2xey-1=0
解之,
乃有
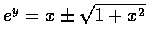 .
但 ey>0 恆成立. 故式中只能取正號.
乃有
.
但 ey>0 恆成立. 故式中只能取正號.
乃有
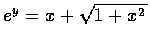 .
這便是說
.
這便是說
將這公式兩邊微分, 乃得
這公式也可以改寫成不定積分的形式如下:
B. 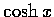 當 x<0 時是狹義減函數,
當
當 x<0 時是狹義減函數,
當 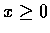 時是狹義增函數.
所以當 x=0 時,
時是狹義增函數.
所以當 x=0 時, 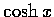 取得極小值 1.
我們把
取得極小值 1.
我們把 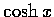 的定義域限制在
的定義域限制在
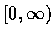 .
令
.
令
則
e2y-2xey+1=0.
解之, 乃有
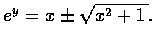 但當 x>1 時
但當 x>1 時
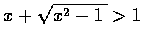 ,
而
,
而
因 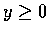 ,
故有
,
故有
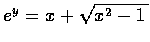 .
這便是說
.
這便是說
將這公式兩邊微分, 乃得
這公式也可以改寫成不定積分的形式如下:
C. 讀者可自行驗證 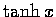 是增函數,其值在 (-1,1) 內.
令
是增函數,其值在 (-1,1) 內.
令
則
(1-x)e2y=1+x.
解之乃有
將上式兩邊微分,遂有
這公式也可以改寫成不定積分的形成如下:
事實上這公式僅當 |x|<1 時成立. 若 |x|>1,
則此積分可用
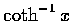 表示,
讀者可自行導出. 但從以上討論的過程中, 我們也得到
表示,
讀者可自行導出. 但從以上討論的過程中, 我們也得到
而這公式對一切 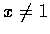 都成立.
都成立.
習

題
- 1.
- (a) 設
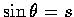 ,
試證必有一整數 n,
使
,
試證必有一整數 n,
使
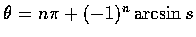 .
.
(b) 設
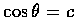 ,
試證必有一整數 n, 使
,
試證必有一整數 n, 使
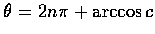 或
或
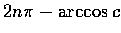 .
.
(c) 設
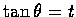 ,
試證必有一整數 n, 使
,
試證必有一整數 n, 使
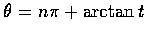 .
(d) 試求出有關其他三個反三角函數的類似結果.
.
(d) 試求出有關其他三個反三角函數的類似結果.
- 2.
- 設
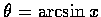 .
試將
.
試將
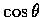 ,
,
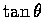 ,
,
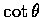 ,
,
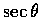 ,
,
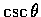 表示成 x 的函數.
表示成 x 的函數.
- 3.
- 求下列諸函數的導函數, 每題需有計算過程:
(a)
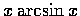 ,
(b)
,
(b)
![$\arccos[(2x+1)^2]$](img155.gif) ,
(c)
,
(c)
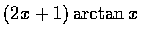 ,
,
(d)
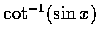 ,
(e)
,
(e)
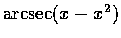 ,
(f)
,
(f)
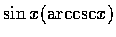 ,
,
(g)
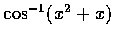 .
.
- 4.
- 令
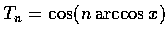 ,
式中
,
式中
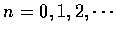 試證
試證
(1-x2)Tn''(x)-xTn'(x)+n2Tn(x)=0.
註. Tn(x) 叫做第一種 n 階 Tchebycheff 多項式.
- 5.
- 函數
叫做 x 的 Gudermannian. 試證
(a)
 .
.
(b)
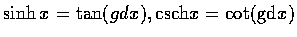 ,
,
(c)
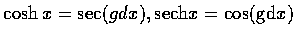 ,
,
(d)
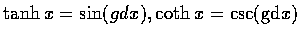 ,
,
(e)
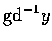 存在, 且等於
存在, 且等於
註. Gudermann 引入函數
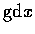 的目的是利用
的目的是利用
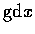 的函數表配合三角函數表以查出 hyperbolic functions 的值.
的函數表配合三角函數表以查出 hyperbolic functions 的值.



Next: 均值定理
Up: 高中單變數微積分的補充
Previous: 有關反三角函數的一些積分公式
1999-06-27
![]() 的導函數
的導函數 ![]() 到處為正,
所以它是一個狹義增函數. 不須縮減它的定義域便可定義其反函數.
這時的問題便是給定 x 要解 y 的方程式
到處為正,
所以它是一個狹義增函數. 不須縮減它的定義域便可定義其反函數.
這時的問題便是給定 x 要解 y 的方程式
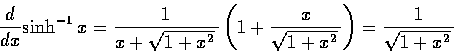
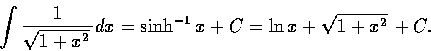
![]() 當 x<0 時是狹義減函數,
當
當 x<0 時是狹義減函數,
當 ![]() 時是狹義增函數.
所以當 x=0 時,
時是狹義增函數.
所以當 x=0 時, ![]() 取得極小值 1.
我們把
取得極小值 1.
我們把 ![]() 的定義域限制在
的定義域限制在
![]() .
令
.
令
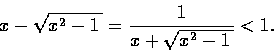
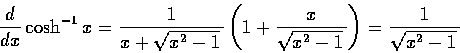
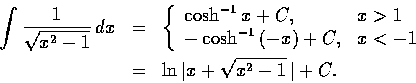
![]() 是增函數,其值在 (-1,1) 內.
令
是增函數,其值在 (-1,1) 內.
令