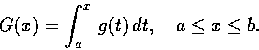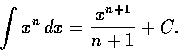
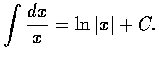
有時不定積分不易計算, 必須稍加變化, 有時積分的計算須分款討論. 以下是一個這種例子:
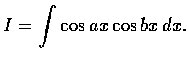
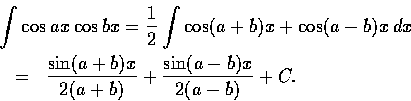
至於定積分, 理科數學課本中曾敘述過微積分基本定理 (Fundamental Theorem of Calculus), 但沒有給證明. 這定理的敘述如下:
定理.
設 f(x) 是 [a, b] 上的連續函數.
若 F(x) 是 f 的一個即
F'(x)=f(x),則
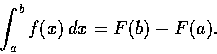
此定理讀者請參考本節末習題的提示自行證明. 在下編中我們還要介紹一個內容更充實的微積分基本定理.
有了本定理, 若知道一函數的不定積分, 便可立即求得定積分. 以下舉兩個例子:
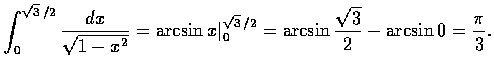
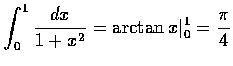
由微積分的基本定理, 只要知道 F 就可計算 F' 的積分, 知道的函數對 (F, F') 越多, 會算的積分也跟著增加, 常見的``積分表''就是收集許多函數對 (F, F') 加以整理而成的. 此外在很多電腦系統上有符號計算的程式, 知名的有 MACSYMA, Mathematica, Derive, Maple V 等都可幫助計算不定積分. 這些現成的工具固然很好, 但是一些基本方法卻是更重要的. 有了這些方法, 纔可以直接用紙筆計算積分; 沒有這些方法, 連上述的各項程式都無從設計起. 這些方法包含有: 部分積分、代換、部分分式等, 以下我們將分別介紹.
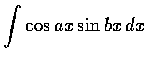 ,
(b)
,
(b)
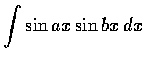 .
.