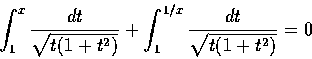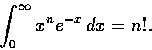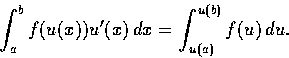
先舉幾個直接代換的簡單例子:
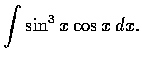
解. 設
![]() ,
則
,
則
![]() .
.
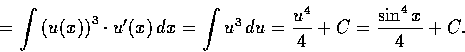
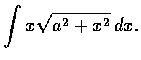
解. 設
u(x) = a2 + x2, 則
u'(x) = 2x.
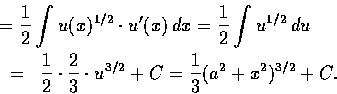
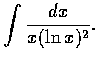
解. 令 ![]() .
則原式 =
.
則原式 =
![]()
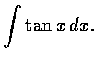
解. 設
![]() ,
則
,
則
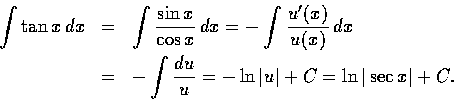
再舉一些引入新變數的例子.
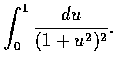
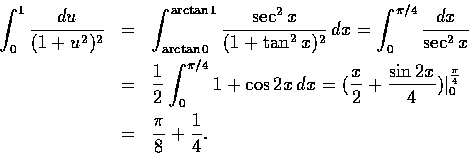
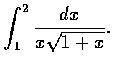
解. 設
![]() ,
即 x = y2-1, 則
dx/dy = 2y. 於是
,
即 x = y2-1, 則
dx/dy = 2y. 於是
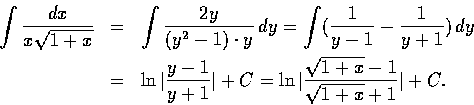
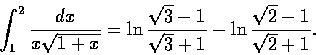
在上面的計算過程中, 我們利用到一個技巧
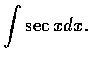
本題的正規解法見第五節, 現在介紹一個偷巧的解法:

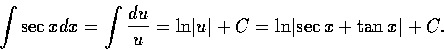
我們所以說這是個偷巧的解法, 原因是變數 u 的設定, 有賴於先知道了答案; 在不先知道答案的情況下, 誰會有這麼大的本領這樣代換呢?
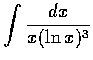 ,
(b)
,
(b)
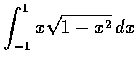 ,
(c)
,
(c)
 (d)
(d)
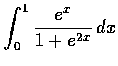 ,
(e)
,
(e)
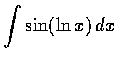 .
.
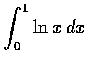 ,
(b)
,
(b)
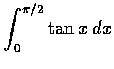 ,
(c)
,
(c)
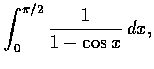 (d)
(d)
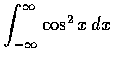 ,
(e)
,
(e)
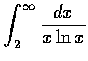 ,
(f)
,
(f)
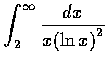 .
.