


Next: 更多代換的例子
Up: 積分技巧
Previous: 三角函數的有理式的積分
以前討論有理函數的積分時, 曾提到下面公式:
設
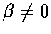 ,
,
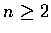 .
則
.
則
這式子並沒完全算出所要的積分, 但若 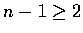 ,
則右邊第二項可再利用 (1) 化簡,
這步驟可繼續進行,
直到出現
,
則右邊第二項可再利用 (1) 化簡,
這步驟可繼續進行,
直到出現
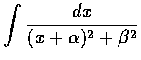 形式的積分. 而
形式的積分. 而
所以反覆利用 (1) 再配合 (2), 我們可算出一般的
![$\displaystyle\int \frac{dx}{[(x+\alpha)^2+\beta^2]^n}$](img160.gif) .
.
公式 (1) 是個遞迴公式 (recursion formula 或 reduction formula) 的例子,
這種情形在解一般積分的問題時常常出現, 以下是一些別的例子:
例 27
設整數
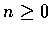
.
試證明
證明. n=0 及 n=1 時本公式顯然成立, 底下考慮 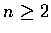 的情形, 此時
的情形, 此時
移項後整理, 得
例 28
設
n 為正整數, 求
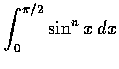
.
解. 若 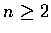 ,
則由例 27 知
,
則由例 27 知
另外,
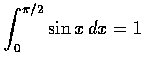 ,
,
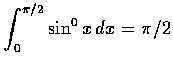 .
所以對一般 n, 反覆利用 (3), 就得答案如下:
.
所以對一般 n, 反覆利用 (3), 就得答案如下:
這些結果叫做 Wallis 公式, 由英國數學家 John Wallis (1616-1703) 引入.
在下篇裡將用它計算 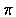 .
.
例 3
設
m 為正整數,
x>0, 且
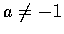
,
試證
證明. 由部分積分法得
明所欲證.
習

題
- 1.
- Evaluate the following integrals:(a)
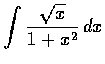 ,
(b)
,
(b)
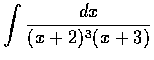 ,(c)
,(c)
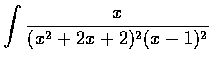 ,(d)
,(d)
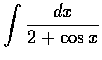 ,
(e)
,
(e)
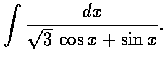
- 2.
- Find each of the following definite integrals: (a)
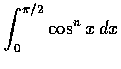 ,
(b)
,
(b)
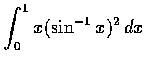 ,(c)
,(c)
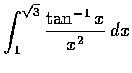 ,
(d)
,
(d)
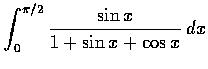 .
.
- 3.
- Obtain recursion formulas for the following integrals: (a)
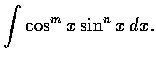 (b)
(b)
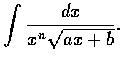
- 4.
- Find the following indefinite integrals: (a)
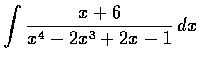 ,
(b)
,
(b)
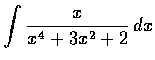 ,(c)
,(c)
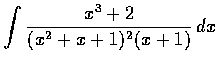 .
.
- 5.
- (a) Show that the substitution
 can convert the integral
of any rational function in x of the hyperbolic functions into the
integral of a rational function in t.(b) Use (a) to compute
can convert the integral
of any rational function in x of the hyperbolic functions into the
integral of a rational function in t.(b) Use (a) to compute
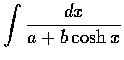 .
.
- 6.
- Show that
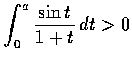 if a>0.
if a>0.



Next: 更多代換的例子
Up: 積分技巧
Previous: 三角函數的有理式的積分
1999-06-27
![\begin{displaymath}\begin{array}{l}
\displaystyle\int \frac{dx}{[(x+\alpha)^2+\b...
... \frac{dx}{[(x+\alpha)^2+\beta ^2]^{n-1}}.
\end{array}\eqno(1)
\end{displaymath}](img156.gif)
![\begin{displaymath}\begin{array}{l}
\displaystyle\int \frac{dx}{[(x+\alpha)^2+\b...
... \frac{dx}{[(x+\alpha)^2+\beta ^2]^{n-1}}.
\end{array}\eqno(1)
\end{displaymath}](img156.gif)
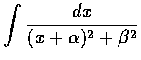 形式的積分. 而
形式的積分. 而
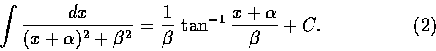
![$\displaystyle\int \frac{dx}{[(x+\alpha)^2+\beta^2]^n}$](img160.gif) .
.
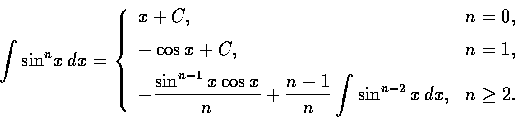
![]() 的情形, 此時
的情形, 此時
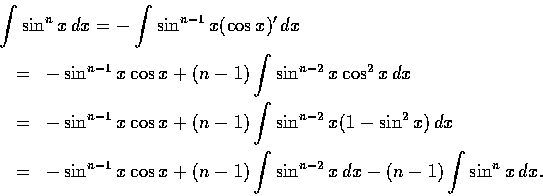
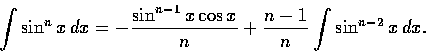
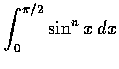 .
.![]() ,
則由例 27 知
,
則由例 27 知
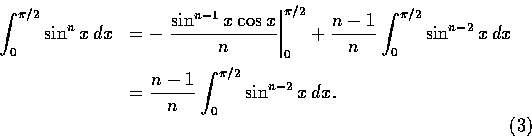
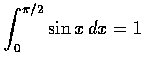 ,
,
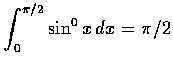 .
所以對一般 n, 反覆利用 (3), 就得答案如下:
.
所以對一般 n, 反覆利用 (3), 就得答案如下:
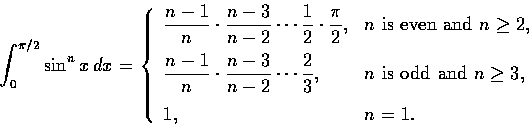
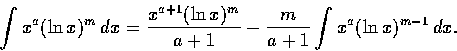
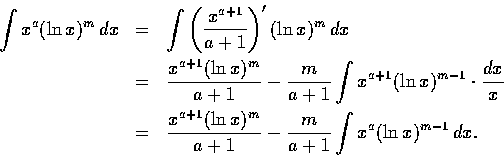
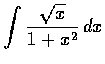 ,
(b)
,
(b)
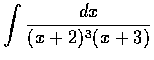 ,(c)
,(c)
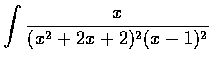 ,(d)
,(d)
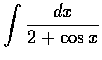 ,
(e)
,
(e)
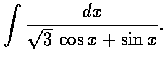
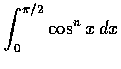 ,
(b)
,
(b)
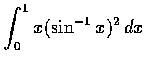 ,(c)
,(c)
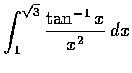 ,
(d)
,
(d)
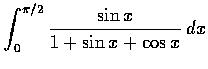 .
.
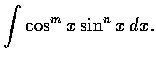 (b)
(b)
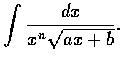
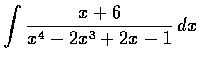 ,
(b)
,
(b)
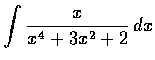 ,(c)
,(c)
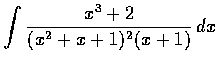 .
.
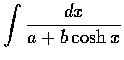 .
.
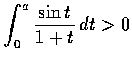 if a>0.
if a>0.