


Next: �T���V�q���~�n
Up: �L�n�����X������
Previous: �L�n�����X������
�] n �������. �ڭ̷Q�n�w�q n��(�ڤ�)�Ŷ��M�䤤���V�q.
�ڭ̥ͬ����g��Ȥκ��Ƥ��W�L3���Ŷ�. �b�����ҥ���,
2 ���M 3 �����V�q���O�δX��k�w�q��.
���ޤJ�y�жb��, �C��2���Ŷ����I����Ӯy��,
�C�� 2 ���V�q����Ӥ��q, �ӨC�� 3 ���Ŷ����I���T�Ӯy��,
�C�� 3 ���V�q���T�Ӥ��q.
�]�� 2 �� 3 ���Ŷ����I�����Ѩ�y�ШM�w, �ӦV�q�]�����Ѩ���q�M�w,
�q�N�ƪ��[�I, �L�y�Ф]�n, ���q�]�n, ���u�O��ƹ�ΤT��Ʋ�,
����W�S�����P; ���զ��I���y�ЩΦV�q�����q��, ��t���P������Ӥw.
�b�����ҥ��٦��@���[���i�ѧڭ̧Q��, ���K�O 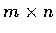 �x�}.
�ڭ̥�
�x�}.
�ڭ̥�
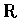 ���ܩҦ���ƪ����X,
���ܩҦ���ƪ����X,
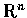 ���ܩҦ����
���ܩҦ���� 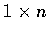 �x�}�����X,
�٤��� n ���Ŷ� (n-dimensional space).
�x�}�����X,
�٤��� n ���Ŷ� (n-dimensional space).
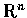 �����������L�O n �ӹ�ƫ��@�w�����DZƦ��@�C�Ӥw.
�H�U�ڭ̤��O�q�V�q���[�I�M�I���[�I�ӰQ��
�����������L�O n �ӹ�ƫ��@�w�����DZƦ��@�C�Ӥw.
�H�U�ڭ̤��O�q�V�q���[�I�M�I���[�I�ӰQ��
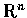 .
.
�b�����ҥ������Q�L3���V�q���غعB��. �ڭ̭n��o���[�����s�� n ��
�h. �]
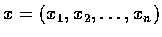 ��
��
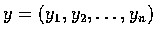 ��
��
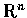 ������Ӥ���.
������Ӥ���.
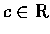 .
�O
.
�O
�h x+y, cx, (c,x) ���O�٬� x �P y ���M, x �� c ��,
�� x �P y �����n (inner product).
�`�N x+y �M cx ���w�q�P�x�}���[�k�P���Ʃw�q�����@�P.
�]�����n (x,y) ���ɤ]�� 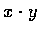 ����, �b�^�夤���]�s dot product.
�T���V�q�Ŷ����o�ǹB��Һ������k�h,
�b n ���V�q�Ŷ��������M����Ū�̸զۦ��Ҥ�.
���ڭ̦b
����, �b�^�夤���]�s dot product.
�T���V�q�Ŷ����o�ǹB��Һ������k�h,
�b n ���V�q�Ŷ��������M����Ū�̸զۦ��Ҥ�.
���ڭ̦b
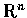 ���Ҽ{�o�ǹB���,
���K�s�@ n ���V�q�Ŷ�(n-dimensional vector space),
�䤤�������s�@ n ���V�q. �Y
���Ҽ{�o�ǹB���,
���K�s�@ n ���V�q�Ŷ�(n-dimensional vector space),
�䤤�������s�@ n ���V�q. �Y
![$x=(x_{1},x_{2},\ldots,x_{n})\in [\mathbb{R} ]^{n}$](img12.gif) ,
�h���
,
�h���
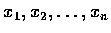 �s�@�������q (components).
�C�Ӥ��q���O 0 ���V�q�s�@�s�V�q (null vector), �ڭ̤]�� 0 ���ܥ�.
�s�@�������q (components).
�C�Ӥ��q���O 0 ���V�q�s�@�s�V�q (null vector), �ڭ̤]�� 0 ���ܥ�.
�Y x �� n ���V�q�h (x,x) ������ڥs�@������ (magnitude,norm),
�H 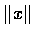 �� |x| ����. �Y�G�V�q������ 1, �h�ٸӦV�q����� (unit) �V�q.
�Y
�� |x| ����. �Y�G�V�q������ 1, �h�ٸӦV�q����� (unit) �V�q.
�Y 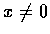 ,�h
,�h
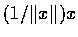 ���P x �P��V�����V�q.
���P x �P��V�����V�q.
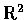 �������V�q u ���i�H���@
�������V�q u ���i�H���@
����, ���� 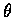 �� u �M x �b������. �Y u ��
�� u �M x �b������. �Y u ��
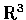 �������V�q,
�O
�������V�q,
�O 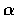 ,
,
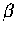 ,
,
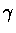 �� u �M�T�y�жb��������,
�h u �b�T�y�Y�жb�W����v���O��
�� u �M�T�y�жb��������,
�h u �b�T�y�Y�жb�W����v���O��
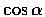 ,
,
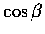 ,
,
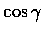 .
�o�T�Ӽƥs�� u ����V�l�� (directional cosines) �� u �i�H����
.
�o�T�Ӽƥs�� u ����V�l�� (directional cosines) �� u �i�H����
�䦸�ڭ̱q�I�������Ӭ� Rn. �b2����3���Ŷ���,
�I�]�O�� 2 �� 3 �ӹ�� (�Y��y��) ���ܪ�.
���s�찪������, �ڭ̤]�� n ����Ʀ�ݦ��I.
�o���I�Һc�������X�٬� n ���Ŷ�, ����
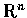 ����.
�]
����.
�]
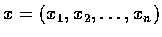 ���@�I. �p�G�� x �ݦ� n ���V�q,
�K�٤����Ӯy�ЦV�q (coordinate vector).
�y�ЦV�q�� 0 ���I�s�� Rn �����I.
�] A, B �����I, ��y�ЦV�q���O�� x, y.
�h y-x ��N���H A ���_�I, �H B �����I���V�q,
���ɥ�
���@�I. �p�G�� x �ݦ� n ���V�q,
�K�٤����Ӯy�ЦV�q (coordinate vector).
�y�ЦV�q�� 0 ���I�s�� Rn �����I.
�] A, B �����I, ��y�ЦV�q���O�� x, y.
�h y-x ��N���H A ���_�I, �H B �����I���V�q,
���ɥ�
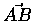 �Ӫ���.
A, B �������Z���w��
�Ӫ���.
A, B �������Z���w�� 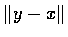 ,
�q�`�H AB ����.
�b n ���Ŷ����P�ɦҼ{�o�Z����, ���K�@ n ���ڤ�Ŷ� (Eulidean space).
���M n ���Ŷ��M n ���ڤ�Ŷ��b�����W���@��,
���ݦ����X�ɥ��̳��O n ���Ŷ������P���V.
��
,
�q�`�H AB ����.
�b n ���Ŷ����P�ɦҼ{�o�Z����, ���K�@ n ���ڤ�Ŷ� (Eulidean space).
���M n ���Ŷ��M n ���ڤ�Ŷ��b�����W���@��,
���ݦ����X�ɥ��̳��O n ���Ŷ������P���V.
��
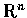 �ݦ��V�q�Ŷ�, �h�������� x, y ���h�� x+y, x-y,
�ݦ��V�q�Ŷ�, �h�������� x, y ���h�� x+y, x-y,
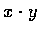 ���B��, �S���V�q����������.
��
���B��, �S���V�q����������.
��
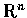 �ݦ��ڤ�Ŷ�, �h�i�H�Q��
�ݦ��ڤ�Ŷ�, �h�i�H�Q��
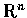 ���I�����Z��,
���I�M�I���వ�[�k, ��k���B��. �]���ڭ̩T�N��Ÿ��V��,
�ҥH�Y x, y ��
���I�����Z��,
���I�M�I���వ�[�k, ��k���B��. �]���ڭ̩T�N��Ÿ��V��,
�ҥH�Y x, y ��
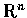 ��������I, a, b ����ӹ��,
�h ax+by �i�H�N���H ax+by ���y�ЦV�q���I.
�H��ڭ̱`�`�o�˥�.
�Ҧp�b���U�Q�u�q�M���u�ɴN�n�p�������b 2 �� 3 ���Ŷ�, ���n�P����.
��v���K�����Y, �����ҵ{�w������, ��n�I�p�U:
�] A �M B ��
��������I, a, b ����ӹ��,
�h ax+by �i�H�N���H ax+by ���y�ЦV�q���I.
�H��ڭ̱`�`�o�˥�.
�Ҧp�b���U�Q�u�q�M���u�ɴN�n�p�������b 2 �� 3 ���Ŷ�, ���n�P����.
��v���K�����Y, �����ҵ{�w������, ��n�I�p�U:
�] A �M B ��
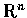 �����I, ��y�ЦV�q���O�� x �M y.
�h���X
�����I, ��y�ЦV�q���O�� x �M y.
�h���X
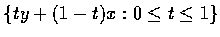 ���ܽu�q AB,
�Ӷ��X
���ܽu�q AB,
�Ӷ��X
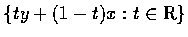 ��
��  �ɪ��ܳs�� AB �����u.
���Y A �M B �����O���I O(�Y
�ɪ��ܳs�� AB �����u.
���Y A �M B �����O���I O(�Y
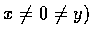 ,
�O
,
�O 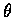 ���� OA �M OB ������, �h
���� OA �M OB ������, �h
�� OA �b OB �W����v��
�O D ���H
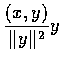 ���y�ЦV�q���I.
D �Y A �b OB �W����v,
�O OB �M A �Z���̵u���a��.
���y�ЦV�q���I.
D �Y A �b OB �W����v,
�O OB �M A �Z���̵u���a��.
�� 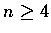 ��, ���A��u���ϥ�
��, ���A��u���ϥ�
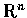 ,
�i�O�o�ǴX�����̵M�Z�q,
�ЬݤU��������:
�] A, B �O
,
�i�O�o�ǴX�����̵M�Z�q,
�ЬݤU��������:
�] A, B �O
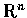 ���G�I, ��y�ЦV�q���O�� X �M Y. �O
���G�I, ��y�ЦV�q���O�� X �M Y. �O
�U�夤�ڭ̱N�ҩ� L(t) �O�s�� A, B �G�I�����u�����׳̵u��,
�ӥB L(t) ������n�O A �M B ���Z�� 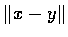 (��
(�� 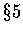 �� 12).
�٥i�ҩ�
�� 12).
�٥i�ҩ�
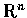 �����N�I C ���y�ЦV�q�O�_�b L(t) �W,
�ݵ� AC+CB=AB �O�_���ߦөw(�����D 1).
�]���ڭ̧� AB �u�q�w��
�����N�I C ���y�ЦV�q�O�_�b L(t) �W,
�ݵ� AC+CB=AB �O�_���ߦөw(�����D 1).
�]���ڭ̧� AB �u�q�w��
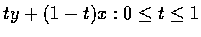 .
�Y
.
�Y 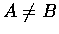 ,
�h A, B �ҨM�w�����u�۵M�N�w��
,
�h A, B �ҨM�w�����u�۵M�N�w��
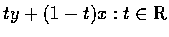 �F
(�Ѭݲ��D2).
�o�˩w�q�����ŦX�ڭ̹�u�q�M���u�����[�{��,
���u�O���W�M
�F
(�Ѭݲ��D2).
�o�˩w�q�����ŦX�ڭ̹�u�q�M���u�����[�{��,
���u�O���W�M
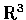 ���������Ӥw.
���������Ӥw.
�A���w A �M B �����O���I (�Y
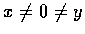 ),
��v�����D�۷���� OB ���u�W�M A �̱����I.
�] OB �u�W���@�I��
),
��v�����D�۷���� OB ���u�W�M A �̱����I.
�] OB �u�W���@�I��
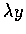 ,
�h
,
�h
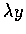 �M A ���Z����
�M A ���Z����
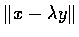 .
�p�U��²�檺�N�ƭp��N�i�M�w
.
�p�U��²�檺�N�ƭp��N�i�M�w
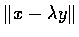 ���̤p�ȩҦb. �]
���̤p�ȩҦb. �]
��M��
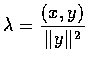 ��,
��,
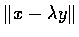 ���o�̤p��.
�] D ���H
���o�̤p��.
�] D ���H
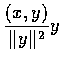 ���y�ЦV�q���I.
D �٬� A �b OB �W����v(projection),
�� OD �٬� OA �b OB �W����v;
�]�i�H��
���y�ЦV�q���I.
D �٬� A �b OB �W����v(projection),
�� OD �٬� OA �b OB �W����v;
�]�i�H��
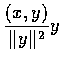 �� x �b y ��V����v.
�S����
�� x �b y ��V����v.
�S����
�G��������
�o�K�O���W�� Cauchy ������. �b�o���������������ߪ��R�n������M�O
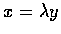 �{�b��
�{�b��
![$\theta\in{[0,\pi]}$](img51.gif) ,
��
,
��
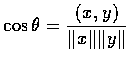 �h OA �b OB �W����v��
�h OA �b OB �W����v��
�p�� 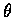 �i���� OA �M OB ������. ���p
�i���� OA �M OB ������. ���p
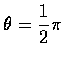 ,
�Y(x,y)=0, �h�� x �M y ����
(per-pendicular) ������ (orthogonal).
���F��K�_��, �ڭ̻{���s�V�q�M�Ҧ��V�q������.
�Y
,
�Y(x,y)=0, �h�� x �M y ����
(per-pendicular) ������ (orthogonal).
���F��K�_��, �ڭ̻{���s�V�q�M�Ҧ��V�q������.
�Y 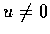 ��
��
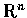 �����V�q,
�h�P u �P��V�����V�q
�����V�q,
�h�P u �P��V�����V�q 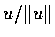 ���Ѥ��V�q�K�O
u �M�Ѯy�жb���������l��, �ڭ̤��٤��� u ����V�l��.
�H�W�ڭ̦b
���Ѥ��V�q�K�O
u �M�Ѯy�жb���������l��, �ڭ̤��٤��� u ����V�l��.
�H�W�ڭ̦b
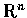 ���i�u�q�B���u�B�����B��v���[��,
���u�A�X���
���i�u�q�B���u�B�����B��v���[��,
���u�A�X���
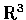 ������, �ӥB�M
������, �ӥB�M
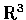 �������[�����ۮe.
Cauchy �������O�W���p�⤤�̭��n�����G, �ڭ̯S�a�N���Ωw�z���Φ����X:
�������[�����ۮe.
Cauchy �������O�W���p�⤤�̭��n�����G, �ڭ̯S�a�N���Ωw�z���Φ����X:
![\begin{theorem}$($\emph{Cauchy ineqiality}$)$ . �] $x,y\in{{\mathbb{R} }^{n}}$ ,...
...y=0$\space �� $\lambda\in{\mathbb{R} }$\space �� $x=\lambda y$ .
\end{theorem}](img57.gif)
�U�����w�z�O�j�媺����w�z (Pythagoras theorem) �����s, ��Ū�̦ۤv�ҩ�.
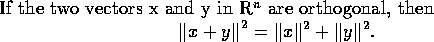
�H�U�X�ӵ��G���i�q Cauchy �������o��:
![\begin{theorem}$($\emph{�T��������}$)$ . �] $x,y\in R^n$ , �h
\begin{displayma...
...����O $x=0$ , ���@��� $\lambda\geq{0}$ ,
�ϱo $y=\lambda{x}$ .
\end{theorem}](img59.gif)
�ҩ�. �q Cauchy �������o
����}��, �K�i�o��ҨD��������.
�Y��������, �h
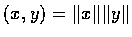 ,
�q�ө� x=0, �Φ��@�����
,
�q�ө� x=0, �Φ��@����� 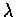 �b,
��
�b,
��
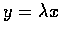 .
�Ϥ��Y������, �h���Ҥ���������������.
.
�Ϥ��Y������, �h���Ҥ���������������.
�o�������K�s���T���Τ����� (triangle inequality). �Q�Υ�, �ڭ̥ߧY�o��
![\begin{theorem}�] $A$ , $B$ , $C$\space �� $\mathbb{R} ^n$\space ���T�I. �h\\
�...
... , $B$ , $C$\space �T�I�@�u,
�B $B$\space �b $A$ , $C$\space ����.
\end{theorem}](img64.gif)
�b���w�z���ҦC�|���Z�����T�өʽ褤, ���]�s���T���Τ�����.
�o�˱o�쪺�Z���M�ڭ̪����[�D�`����.
�]���ڭ̻{��
 ���Z�����[���O 2 �� 3 ���Ŷ����Z���[�����۵M���s.
���Z�����[���O 2 �� 3 ���Ŷ����Z���[�����۵M���s.



Next: �T���V�q���~�n
Up: �L�n�����X������
Previous: �L�n�����X������
1999-06-27
![]() �x�}.
�ڭ̥�
�x�}.
�ڭ̥�
![]() ���ܩҦ���ƪ����X,
���ܩҦ���ƪ����X,
![]() ���ܩҦ����
���ܩҦ���� ![]() �x�}�����X,
�٤��� n ���Ŷ� (n-dimensional space).
�x�}�����X,
�٤��� n ���Ŷ� (n-dimensional space).
![]() �����������L�O n �ӹ�ƫ��@�w�����DZƦ��@�C�Ӥw.
�H�U�ڭ̤��O�q�V�q���[�I�M�I���[�I�ӰQ��
�����������L�O n �ӹ�ƫ��@�w�����DZƦ��@�C�Ӥw.
�H�U�ڭ̤��O�q�V�q���[�I�M�I���[�I�ӰQ��
![]() .
.
![]() ��
��
![]() ��
��
![]() ������Ӥ���.
������Ӥ���.
![]() .
�O
.
�O
![]() �� |x| ����. �Y�G�V�q������ 1, �h�ٸӦV�q����� (unit) �V�q.
�Y
�� |x| ����. �Y�G�V�q������ 1, �h�ٸӦV�q����� (unit) �V�q.
�Y ![]() ,�h
,�h
![]() ���P x �P��V�����V�q.
���P x �P��V�����V�q.
![]() �������V�q u ���i�H���@
�������V�q u ���i�H���@
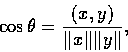
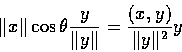
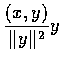 ���y�ЦV�q���I.
D �Y A �b OB �W����v,
�O OB �M A �Z���̵u���a��.
���y�ЦV�q���I.
D �Y A �b OB �W����v,
�O OB �M A �Z���̵u���a��.
![]() ��, ���A��u���ϥ�
��, ���A��u���ϥ�
![]() ,
�i�O�o�ǴX�����̵M�Z�q,
�ЬݤU��������:
�] A, B �O
,
�i�O�o�ǴX�����̵M�Z�q,
�ЬݤU��������:
�] A, B �O
![]() ���G�I, ��y�ЦV�q���O�� X �M Y. �O
���G�I, ��y�ЦV�q���O�� X �M Y. �O
![]() ),
��v�����D�۷���� OB ���u�W�M A �̱����I.
�] OB �u�W���@�I��
),
��v�����D�۷���� OB ���u�W�M A �̱����I.
�] OB �u�W���@�I��
![]() ,
�h
,
�h
![]() �M A ���Z����
�M A ���Z����
![]() .
�p�U��²�檺�N�ƭp��N�i�M�w
.
�p�U��²�檺�N�ƭp��N�i�M�w
![]() ���̤p�ȩҦb. �]
���̤p�ȩҦb. �]
![\begin{eqnarray*}{\Vert x-\lambda{y}\Vert}^{2}&=&\Vert x\Vert^{2}-2(x,y)\lambda+...
...Vert x\Vert^{2}-{ \left[\frac{(x,y)}{\Vert y\Vert} \right]}^{2}.
\end{eqnarray*}](img46.gif)
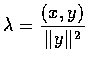 ��,
��,
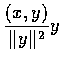 ���y�ЦV�q���I.
D �٬� A �b OB �W����v(projection),
�� OD �٬� OA �b OB �W����v;
�]�i�H��
���y�ЦV�q���I.
D �٬� A �b OB �W����v(projection),
�� OD �٬� OA �b OB �W����v;
�]�i�H��
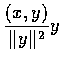 �� x �b y ��V����v.
�S����
�� x �b y ��V����v.
�S����
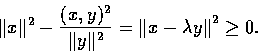
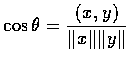 �h OA �b OB �W����v��
�h OA �b OB �W����v��
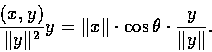
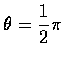 ,
�Y(x,y)=0, �h�� x �M y ����
(per-pendicular) ������ (orthogonal).
���F��K�_��, �ڭ̻{���s�V�q�M�Ҧ��V�q������.
�Y
,
�Y(x,y)=0, �h�� x �M y ����
(per-pendicular) ������ (orthogonal).
���F��K�_��, �ڭ̻{���s�V�q�M�Ҧ��V�q������.
�Y ![\begin{theorem}$($\emph{Cauchy ineqiality}$)$ . �] $x,y\in{{\mathbb{R} }^{n}}$ ,...
...y=0$\space �� $\lambda\in{\mathbb{R} }$\space �� $x=\lambda y$ .
\end{theorem}](img57.gif)
![]()
![\begin{theorem}$($\emph{�T��������}$)$ . �] $x,y\in R^n$ , �h
\begin{displayma...
...����O $x=0$ , ���@��� $\lambda\geq{0}$ ,
�ϱo $y=\lambda{x}$ .
\end{theorem}](img59.gif)
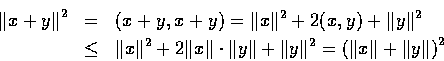
![]() ,
�q�ө� x=0, �Φ��@�����
,
�q�ө� x=0, �Φ��@����� ![]() �b,
��
�b,
��
![]() .
�Ϥ��Y������, �h���Ҥ���������������.
.
�Ϥ��Y������, �h���Ҥ���������������.
![\begin{theorem}�] $A$ , $B$ , $C$\space �� $\mathbb{R} ^n$\space ���T�I. �h\\
�...
... , $B$ , $C$\space �T�I�@�u,
�B $B$\space �b $A$ , $C$\space ����.
\end{theorem}](img64.gif)
![]() ���Z�����[���O 2 �� 3 ���Ŷ����Z���[�����۵M���s.
���Z�����[���O 2 �� 3 ���Ŷ����Z���[�����۵M���s.