


Next: 向量值函數與曲線
Up: 微積分的幾何應用
Previous: n 維空間與 n 維向量
在
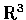 中除了內積外, 還定義有一種外積.
因為外積的定義僅限於三維空間, 所以在本節中我們所談的向量都是三維的.
取二向量
u=(u1,u2,u3),
v=(v1,v2,v3).
我們定義這二向量的外積 (outerproduct 或 cross product) 為
中除了內積外, 還定義有一種外積.
因為外積的定義僅限於三維空間, 所以在本節中我們所談的向量都是三維的.
取二向量
u=(u1,u2,u3),
v=(v1,v2,v3).
我們定義這二向量的外積 (outerproduct 或 cross product) 為
式中
為了便於記憶, 我們常常把此式寫作
這個外積的定義是純代數的. 在本節最後我們會討論到和它相當的幾何定義.
外積不滿足通常體論中的那些定律, 如交換律、結合律等. 但它滿足另外的一些定律,
自成一個系統, 茲條陳如次:
在以上公式中, 設
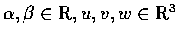 .
以下二公式極易證明:
.
以下二公式極易證明:
從後式可得
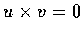 .
.
外積和內積互有關聯: 設
則
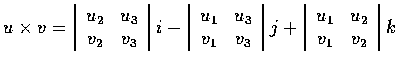 .
.
故
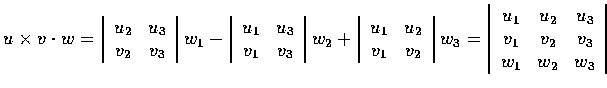 .
從
.
從
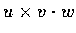 的公式我們立即可以得到
的公式我們立即可以得到
即
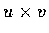 和 u 正交, 和 v 也正交. 本式另一個推論是
和 u 正交, 和 v 也正交. 本式另一個推論是
這是一個很特殊的結合律.
外積不滿足真正的結合律. 設 u,v,w 為三向量,
我們想導出計算
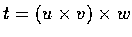 的公式.
令
t=(t1,t2,t3). 因
的公式.
令
t=(t1,t2,t3). 因
故有
同理
乃得下公式:
以下解釋外積的幾何意義. 先計算
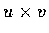 的長.
設 u 和 v 間的夾角為
的長.
設 u 和 v 間的夾角為 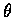 .
則
.
則
於是
乃有
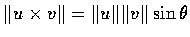 ;
這就是說
;
這就是說
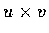 的長等於以 u 和 v 為兩邊的平行四邊形的面積.
再來解釋
的長等於以 u 和 v 為兩邊的平行四邊形的面積.
再來解釋
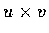 的方向. 設
的方向. 設
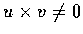 .
則 u, v 決定一平面
.
則 u, v 決定一平面  .
因
.
因
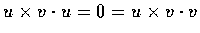 ,
故
,
故
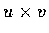 在
在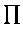 的法線方向.
依平常習慣, 座標系的選擇是使 i=(1,0,0), j=(0,1,0), k=(0,0,1)三向量形成一右手座標系 (或稱右手螺旋系).
因
的法線方向.
依平常習慣, 座標系的選擇是使 i=(1,0,0), j=(0,1,0), k=(0,0,1)三向量形成一右手座標系 (或稱右手螺旋系).
因
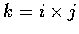 ,
故 i, j,
,
故 i, j,
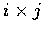 形成右手螺旋系.
同樣情形, j, k,
形成右手螺旋系.
同樣情形, j, k,
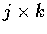 和 k, i,
和 k, i,
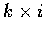 都形成右手螺旋系.
一般情形, 若
都形成右手螺旋系.
一般情形, 若
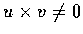 ,
則由定義及我們圖示的習慣, u, v,
,
則由定義及我們圖示的習慣, u, v,
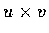 形成右手螺旋系. 故有下面外積的幾何定義:
形成右手螺旋系. 故有下面外積的幾何定義:
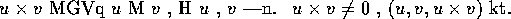
現在讓我們回到
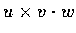 的討論.
設
的討論.
設
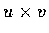 和 w 間的夾角為
和 w 間的夾角為 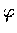 .
考慮以 u,v,w 為三稜的平行六面體 S.
我們取以 u,v 為二邊的平行四邊形為 S 的底邊.
則 S 的高為
.
考慮以 u,v,w 為三稜的平行六面體 S.
我們取以 u,v 為二邊的平行四邊形為 S 的底邊.
則 S 的高為
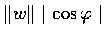 .
因此
.
因此
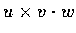 的絕對值為 S 的體積.
若
的絕對值為 S 的體積.
若
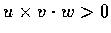 ,
則
,
則
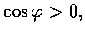 即 w 和
即 w 和
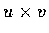 的夾角為銳角;
w 和
的夾角為銳角;
w 和
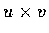 在 u,v 所決定的平面的同一邊,
所以 u,v,w 也形成右手螺旋系.
反之, 若
在 u,v 所決定的平面的同一邊,
所以 u,v,w 也形成右手螺旋系.
反之, 若
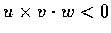 ,
則
,
則
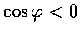 ,
即
,
即 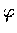 為鈍角;
w 和
為鈍角;
w 和
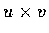 在 u,v 所決定的平面的不同的兩邊,
所以 u,v,w 形成左手螺旋系.
在 u,v 所決定的平面的不同的兩邊,
所以 u,v,w 形成左手螺旋系.
習

題
- 1.
- 設
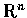 中三點 A,B,C 的座標向量分別為 x,y,z.
中三點 A,B,C 的座標向量分別為 x,y,z.
(a)若
z=ty+(1-t)x, 式中
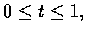 則 AC+CB=AB.
則 AC+CB=AB.
(b)若 AC+CB=AB, 則必有
![$t\in{[0,1]}$](img104.gif) 使
z=ty+(1-t)x.
使
z=ty+(1-t)x.
- 2.
- 設 A,B 為
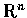 中相異二點, 其座標向量分別為 x,y.
用 L 表示 A,B 所 決定的直線. 試證
中相異二點, 其座標向量分別為 x,y.
用 L 表示 A,B 所 決定的直線. 試證
(a) 若
P1, P2, P3 在 L 上,
則
P1P2, P2P3, P3P1 中最長一段是其餘二段的和.
(b) 若
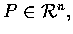 且 AP,BP,AB 三線段中最長一段是其餘二段的和,
則
且 AP,BP,AB 三線段中最長一段是其餘二段的和,
則 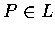 .
.
- 3.
- Let u and v be two non-zero vectors in
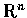 and let
and let
Prove that w makes equal angles with u and v.
- 4.
- 設
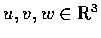 .
試證
.
試證
註. 本公式叫做 Jacobi 恆等式.
- 5.
- Let
f(t)=(f1(t),f2(t),f3(t)) be a vector-valued function
for
![$t\in{[a,b]}$](img110.gif) .
If f is continuous on [a,b] and is differentiable on (a,b),
prove that there is
.
If f is continuous on [a,b] and is differentiable on (a,b),
prove that there is
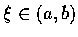 such that the tangent vector of
f at
such that the tangent vector of
f at 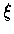 is orthogonal to the vector
is orthogonal to the vector
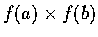 .
.



Next: 向量值函數與曲線
Up: 微積分的幾何應用
Previous: n 維空間與 n 維向量
1999-06-27
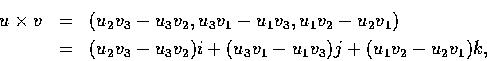
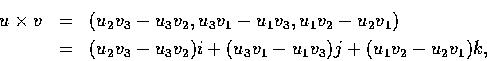
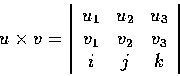
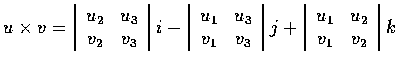 .
.
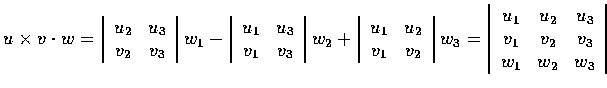 .
從
.
從
![]() 的公式.
令
t=(t1,t2,t3). 因
的公式.
令
t=(t1,t2,t3). 因
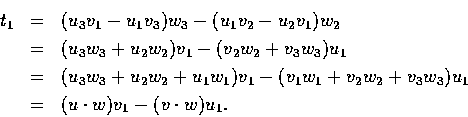
![]() 的長.
設 u 和 v 間的夾角為
的長.
設 u 和 v 間的夾角為 ![]() .
則
.
則
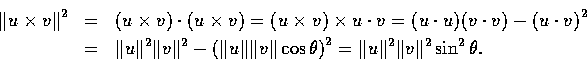
![]() 的討論.
設
的討論.
設
![]() 和 w 間的夾角為
和 w 間的夾角為 ![]() .
考慮以 u,v,w 為三稜的平行六面體 S.
我們取以 u,v 為二邊的平行四邊形為 S 的底邊.
則 S 的高為
.
考慮以 u,v,w 為三稜的平行六面體 S.
我們取以 u,v 為二邊的平行四邊形為 S 的底邊.
則 S 的高為
![]() .
因此
.
因此
![]() 的絕對值為 S 的體積.
若
的絕對值為 S 的體積.
若
![]() ,
則
,
則
![]() 即 w 和
即 w 和
![]() 的夾角為銳角;
w 和
的夾角為銳角;
w 和
![]() 在 u,v 所決定的平面的同一邊,
所以 u,v,w 也形成右手螺旋系.
反之, 若
在 u,v 所決定的平面的同一邊,
所以 u,v,w 也形成右手螺旋系.
反之, 若
![]() ,
則
,
則
![]() ,
即
,
即 ![]() 為鈍角;
w 和
為鈍角;
w 和
![]() 在 u,v 所決定的平面的不同的兩邊,
所以 u,v,w 形成左手螺旋系.
在 u,v 所決定的平面的不同的兩邊,
所以 u,v,w 形成左手螺旋系.