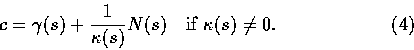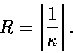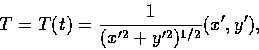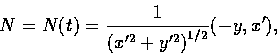Next: 體積
Up: 微積分的幾何應用
Previous: 弧長
設平面曲線
C:(x,y)=r(t), 其中 r(t) 具有連續的導函數,
則稱 C 為平滑 (smooth) 曲線.
若其上一點 P=r(t) 滿足
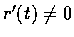 ,
則該點 P 叫作 C 關於參數 t 的正則 (regular) 點.
若 C 的每點都是正則點, 則 t 叫作 C 的正則參數.
在本節以下的討論中, 我們將假定所有的參數都是正則參數.
,
則該點 P 叫作 C 關於參數 t 的正則 (regular) 點.
若 C 的每點都是正則點, 則 t 叫作 C 的正則參數.
在本節以下的討論中, 我們將假定所有的參數都是正則參數.
在一曲線 C 上我們取一定點 A.
另 s 為從 A 沿 C 到 C 上的一點 P 的弧長.
則 s 是曲線的參數的增函數. 因為曲線的參數正則, 這個增函數是狹義的;
它的反函數存在. 於是我們可以用 s 作為曲線的新參數.
設 C 以 s 為參數的參數方程式為
C:r=(f(s),g(s)).
因
ds2=dx2+dy2, 故得
f'(s)2+g'(s)2=1. 令
則 T 和 N 都是單位向量. T 叫作 C 在 P 點的單位切向量,
N 叫作 C 在 P 的單位法 (normal) 向量.
通過 P 沿 T 方向的直線叫作 C 在 P的切線,
通過 P 沿 N 方向的直線叫作 C 在 P 的法線.
從 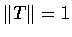 得
得
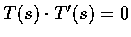 .
因此 T'(s) 為一沿 N(s) 方向的向量. 令
.
因此 T'(s) 為一沿 N(s) 方向的向量. 令
則
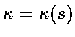 叫作曲線在 P 點處的曲率(curvature).
叫作曲線在 P 點處的曲率(curvature).
Now we return to consider a curve
C:(x,y)=r(t).
with a regular parament t. Assume that r''(t) exists.
Consider three points corresponding to the parameters t0, t1and t2 on this curve.
Let 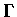 be the circle pass through the points r(t0),
r(t1) and r(t2).
If the center of
be the circle pass through the points r(t0),
r(t1) and r(t2).
If the center of 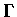 is c and the radius of
is c and the radius of 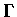 is R, set
is R, set
then
F(t0)=F(t1)=F(t2)=0
By Rolle's theorem, there is a number 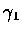 lying between t0 and
T1 and a number
lying between t0 and
T1 and a number 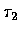 between t1 and t2 such that
between t1 and t2 such that
Another application of Rolle's theorem yields the existence of
a number 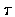 between
between 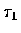 and
and 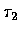 such that
such that
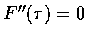 .
When both t1 and t2 approach t0, the limiting
position of
.
When both t1 and t2 approach t0, the limiting
position of 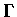 is called the circle of curvature (曲率圓)
of C at
is called the circle of curvature (曲率圓)
of C at
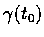 .
Its center c and radius R are called the center of cruvature
(曲率中心) and the radius of curvature (曲率半徑)
of C at
.
Its center c and radius R are called the center of cruvature
(曲率中心) and the radius of curvature (曲率半徑)
of C at
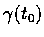 respectively.
As then
respectively.
As then 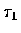 ,
,
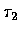 and
and 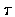 also approch
t0, we see that c and R satisfy the equations
also approch
t0, we see that c and R satisfy the equations
Now considwe C as parametrized by the arc length s from a fixed
pre-assigned point,and consider the circle of curvature 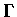 of C at
of C at
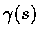 .
Then the equatons F'(s)=0 and F''(s)=0 can be rewritten as
.
Then the equatons F'(s)=0 and F''(s)=0 can be rewritten as
and
respectively. Equation (2) shows that
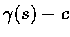 is orthogonal to
T(s), and is thus a constant multiple of N(s).
Set
is orthogonal to
T(s), and is thus a constant multiple of N(s).
Set
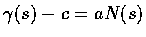 .
Then
.
Then
Finallly from the equation F(s)=0 we get the radius of cruvature
It is customary to say that 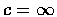 and
and 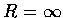 if
if
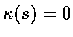 .
.
Our next task is to derive formulas for the center and the radius of curvature
in case C is not parametrized by arc length.
For this we writer
r(t)=(x(t),y(t)).
Then
and
where the derivattives are taken with respect to t. Now
or
This yields the formula
Having this formula for the curvature,
the center and radius of curvature can easily
be obtained form the formulas (4) and (5).
習

題
- 1.
- Prove that the curvature of a plane curve is equal to the rate of change
of the inclination (斜角) of the tangent line to the curve with respect to
the arc length. Conclude that the curvature of a curve is independent of
the particular parameter chosen.
- 2.
- 在曲線
y=6ln(2x+1) 上找出其曲率取得極小值的點.
這曲線上有曲率取得極大值之點否?
- 3.
- 設函數 f(x) 有連續的二階導函數,
f(0)=f'(0)=0, f"(0)>0.
在此曲線上取一點 P 並經過 p 作 OP 的垂線,
交 y 軸於 (0,b). 試以曲線 y=f(x) 在 x=0 處的曲率表出當
p 趨近於原點時 b 的極限.



Next: 體積
Up: 微積分的幾何應用
Previous: 弧長
1999-06-27