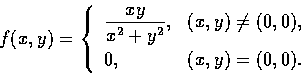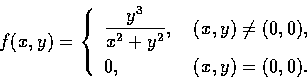Next: 偏導函數
Up: 多變數函數的微分學
Previous: n 變數函數的圖形、曲面
Let
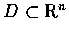 ,
f be a function on D,
,
f be a function on D,
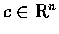 ,
and l a fixed number.
We say that the limit of f(x) is l when
,
and l a fixed number.
We say that the limit of f(x) is l when
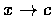 if f(x) gets arbitrarily close to l whenever x,
while remaining distinct from c, gets sufficiently close c .
if f(x) gets arbitrarily close to l whenever x,
while remaining distinct from c, gets sufficiently close c .
這是極限觀念的極粗略的描述, 在下編中我們會有更嚴謹的討論,
和單變數時類似, 若有正數 K 使 c 點附近和 c 相異的點 x 都能滿足
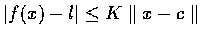 ,
則定義中的條件顯然符合. 於是
,
則定義中的條件顯然符合. 於是
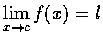 ,
這充分條件是證明一些簡單的極限問題時常用的方法.
,
這充分條件是證明一些簡單的極限問題時常用的方法.
利用極限概念可定義連續概念如次:
Loosely speaking, a function is said to be continuous at point p
if for those values of x where f(x) is defined,
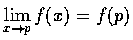 .
f is said to be continuous on the domain D if it is continuous
at every point
.
f is said to be continuous on the domain D if it is continuous
at every point 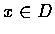 .
.
若
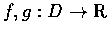 在 p 點連續, 則 f(x)g(x) 及
af(x)+bg(x),
在 p 點連續, 則 f(x)g(x) 及
af(x)+bg(x),
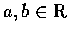 ,
也都在 p 點連續.
至於
,
也都在 p 點連續.
至於
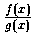 ,
其連續的區域可能縮小,
因為我們可能有將使 g(x)=0 的點排的需要 (見例 3)
,
其連續的區域可能縮小,
因為我們可能有將使 g(x)=0 的點排的需要 (見例 3)
例 1
設
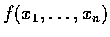
是
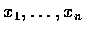
的多項式,
則
f 處處連續.
例 2
Let
Is
f continuous at (0,0)?
Solution. For
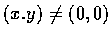 we have
we have
Therefore
f is thus seen to be continuous at (0,0).
例 3
Let
Is
f continuous at (0,0) ?
解. 欲解本問題, 我們考慮 f 在通過原點 (0,0) 的諸直線上的 behavior.
令 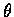 為定角,
滿足
為定角,
滿足
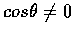 and
and
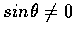 ,
則在直線
,
則在直線
上, 下式成立:
故知
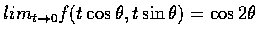 .
因為此值與所論直線織選擇有關, 所以當
.
因為此值與所論直線織選擇有關, 所以當
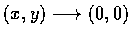 時,
所論之函數沒有極限, 故微在原點 (0,0) 處不連續函數.
時,
所論之函數沒有極限, 故微在原點 (0,0) 處不連續函數.
本例題告訴我們, 若變數沿不同的直線趨於一點時, 函數有不同的極限,
則當變數 (不限制路線) 趨於該點時, 極限不存在.
這例題的逆命題不成立. 讀者可參考下面的第四題. 本例題的另一個有趣的結果是
習

題
- 1.
- 求下列二函數的等高線:
(a)
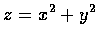 ,
(b)
,
(b)
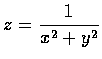 .
.
- 2.
- 描述下列函數的等位面:
(a)
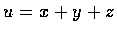 ,
(b)
,
(b)
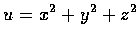 .
.
- 3.
- 計算下列極限之值:
(a)
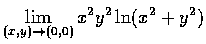 ,(b)
,(b)
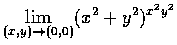 .
.
- 4.
- Consider the function
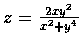 .
Show that z approaches 0when (x,y) moves
along any straight line toward the origin while z approaches
different limits
when (x,y) moves along the two parabolas
.
Show that z approaches 0when (x,y) moves
along any straight line toward the origin while z approaches
different limits
when (x,y) moves along the two parabolas
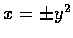 .
.
- 5.
- 設
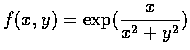 .
問
.
問 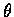 為何值時
為何值時
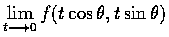 存在?
存在?
- 6.
- Sketch the level curves for the surface whose equation is
z=1+(x2 +y2 ) e-(x2 +y2 ).
Determine the maximum on this surface.
- 7.
- Determium the valuds of the following functions f(x,y)
along the lines y=mx in terms of x. Are they continuous at the origin?
- 8.
- 令
(a) 問
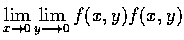 是否存在? 為什麼?
是否存在? 為什麼?
(b) f 在原點是否連續?



Next: 偏導函數
Up: 多變數函數的微分學
Previous: n 變數函數的圖形、曲面
1999-06-28
![]() ,
則定義中的條件顯然符合. 於是
,
則定義中的條件顯然符合. 於是
![]() ,
這充分條件是證明一些簡單的極限問題時常用的方法.
,
這充分條件是證明一些簡單的極限問題時常用的方法.
![]() .
f is said to be continuous on the domain D if it is continuous
at every point
.
f is said to be continuous on the domain D if it is continuous
at every point ![]() .
.
![]() 在 p 點連續, 則 f(x)g(x) 及
af(x)+bg(x),
在 p 點連續, 則 f(x)g(x) 及
af(x)+bg(x),
![]() ,
也都在 p 點連續.
至於
,
也都在 p 點連續.
至於
![]() ,
其連續的區域可能縮小,
因為我們可能有將使 g(x)=0 的點排的需要 (見例 3)
,
其連續的區域可能縮小,
因為我們可能有將使 g(x)=0 的點排的需要 (見例 3)
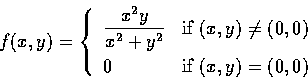
![]() we have
we have
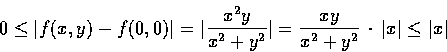
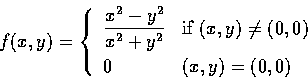
![]() 為定角,
滿足
為定角,
滿足
![]() and
and
![]() ,
則在直線
,
則在直線
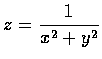 .
.
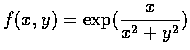 .
問
.
問