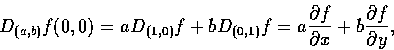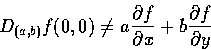Next: Chain Rule and the
Up: 多變數函數的微分學
Previous: Limit and Continuity
在本節中我們討論多變數函數的導函數. 單變數函數的導數可以解釋微函數的變化率.
多變數函數的變化情形會依方向的不同而有差異.
所以討論多變數函數在一點 p 的導函數時, 需要就過 p 的各個曲線考慮.
實際做法如下: 設 D為
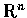 中的一區域, f 為定義在 D 上的函數,
中的一區域, f 為定義在 D 上的函數,
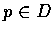 ,
,
為通過 p 的一曲線,
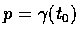 .
若
.
若
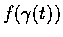 可微, 則
可微, 則
稱為 f 沿 C 在 p 處的函數.
設 u 為
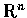 中的向量,
中的向量, 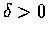 .
假定對一切
.
假定對一切
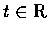 ,
,
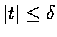 ,
均有
,
均有
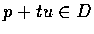 .
考慮線段
.
考慮線段
![$C: x=p+tu,\, t \in [ \delta , \delta ]$](img66.gif) .
則 f 沿 C 在 p 處的導函數稱為 f 在 p 處對 u 的導函數,
以下以 Duf(p) 表示. 換言之,
.
則 f 沿 C 在 p 處的導函數稱為 f 在 p 處對 u 的導函數,
以下以 Duf(p) 表示. 換言之,
假若 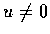 ,
則
,
則
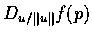 稱為
f 在 p 沿 u 方向的方向導函數 (directional derivative).
因為
Dauf(p)=aDuf(p) 對任意實數 a 均成立,
所以若能知道一函數的諸方向導函數, 則它關於任意向量的導函數便都清楚了.
稱為
f 在 p 沿 u 方向的方向導函數 (directional derivative).
因為
Dauf(p)=aDuf(p) 對任意實數 a 均成立,
所以若能知道一函數的諸方向導函數, 則它關於任意向量的導函數便都清楚了.
若 u 為沿第 k 個座標軸的單位向量,
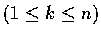 ,
即
,
即
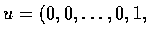
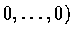 ,
式中的 1 在第 k 個位置, 我們便把 Duf(p) 表成
,
式中的 1 在第 k 個位置, 我們便把 Duf(p) 表成
之形, 而稱之為 partial derivative (偏導函數) of f with respect to
xk at p.
例 4
If
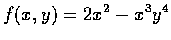
,
calculate
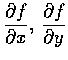
and
Duf(
x,
y) for
u=(
a,
b).
解. 計算
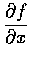 時, 視 y 為參數, 並保持不變. 乃有
時, 視 y 為參數, 並保持不變. 乃有
仿此
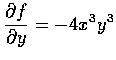 .
對 u=(a,b), 令 (x,y) 為任意定點. 設
.
對 u=(a,b), 令 (x,y) 為任意定點. 設
g(t)=f(x+ta, y+tb)=2(x+ta)2-(x+ta)3 (y+tb)4.
則
Duf(x,y)=g'(0)=4ax-3ax2 y4 -4bx3 y3.
例 5
Let
f(
x,
y)=(
x2 +
y2 )
e-x2 -y2.
Find
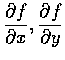
and
D(a, b) f(
x,
y).
Solution. Let u=(a,b) . To calculae
D(a, b)f(x, y) , we put
g(t)=f((x,y)+tu)=[(x+ta)2 +(y+tb)2 ]e-(x+ta)2 -(y+tb)2
Then
Du f(x, y)=g'(0)=2(ax+by)e-x2 -y2 (1-x2 -y2 ).
In particular, if
u=(a,b)=(1,0), we have
and if
u=(a,b)=(0,1), we have
例 6
Let
Compute
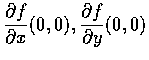
and
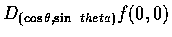
.
Solution. Since
f(x,0) = 0 and
f(0,y) = y,
we have
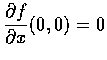 and
and
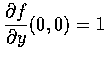 .
Now
.
Now
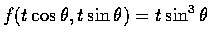 .
Thus
.
Thus
Looking back to these examples, we see immediately that for the functions fin Ex. 4 and Ex. 5, we have
but for the function f in Ex. 6,
if 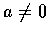 . This problem will be studied in the next section.
. This problem will be studied in the next section.



Next: Chain Rule and the
Up: 多變數函數的微分學
Previous: Limit and Continuity
1999-06-28
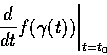
![]() 中的向量,
中的向量, ![]() .
假定對一切
.
假定對一切
![]() ,
,
![]() ,
均有
,
均有
![]() .
考慮線段
.
考慮線段
![]() .
則 f 沿 C 在 p 處的導函數稱為 f 在 p 處對 u 的導函數,
以下以 Duf(p) 表示. 換言之,
.
則 f 沿 C 在 p 處的導函數稱為 f 在 p 處對 u 的導函數,
以下以 Duf(p) 表示. 換言之,
![]() ,
即
,
即
![]()
![]() ,
式中的 1 在第 k 個位置, 我們便把 Duf(p) 表成
,
式中的 1 在第 k 個位置, 我們便把 Duf(p) 表成
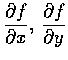 and
Duf(x,y) for u=(a,b).
and
Duf(x,y) for u=(a,b). ![]() 時, 視 y 為參數, 並保持不變. 乃有
時, 視 y 為參數, 並保持不變. 乃有
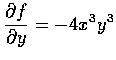 .
對 u=(a,b), 令 (x,y) 為任意定點. 設
.
對 u=(a,b), 令 (x,y) 為任意定點. 設
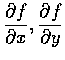 and
D(a, b) f(x, y).
and
D(a, b) f(x, y). 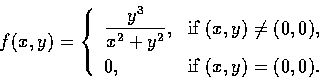
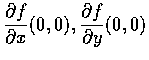 and
and
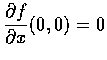 and
and
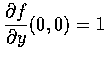 .
Now
.
Now