


Next: Extrema with constraints
Up: 多變數函數的微分學
Previous: Higher Order Derivatives
在高中課程中曾經討論過利用導函數解單變數函數的極大和極小值問題.
現在我們要把這些結果推廣到多變數的函數去.
設
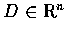 ,
f 為定義在 D 中實數值函數,
a 為 D 的內點. 若有一正數 r 存在, 使當
| x-a | <r 時恆有
,
f 為定義在 D 中實數值函數,
a 為 D 的內點. 若有一正數 r 存在, 使當
| x-a | <r 時恆有
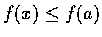 ,
則稱 f 在 x=a 處取得相對 (或局部) 極大值 (relative
or local maximum) f(a). 若將以上討論中的
,
則稱 f 在 x=a 處取得相對 (或局部) 極大值 (relative
or local maximum) f(a). 若將以上討論中的
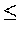 符號改為
符號改為 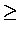 ,
則稱 f 在 x=a 處取得相對
(或局部) 極小值 (relative or local minimum) f(a).
相對極大值和相對極小值統稱相對 (或局部) 極值 (extremum).
在上下文不發生混淆的時候, 相對 (或局部) 的字樣可以省略.
,
則稱 f 在 x=a 處取得相對
(或局部) 極小值 (relative or local minimum) f(a).
相對極大值和相對極小值統稱相對 (或局部) 極值 (extremum).
在上下文不發生混淆的時候, 相對 (或局部) 的字樣可以省略.
若單變數的可微分函數 f(x) 在 x=a 取得相對極值,
則 f'(a)=0. 這結果可以推廣到多變數的函數上去:
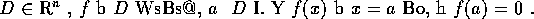
證明. 令
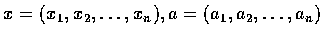 .
設 i 為正整數,
.
設 i 為正整數,
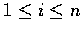 ,
考慮單變數 t 的函數
,
考慮單變數 t 的函數
則 g(t) 在 t=ai 處取得相對極值. 因此 g'(ai)=0,
即
fxi(a)=0. 又因此式對
 均成立, 故
均成立, 故
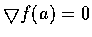 .
明所欲證.
.
明所欲證.
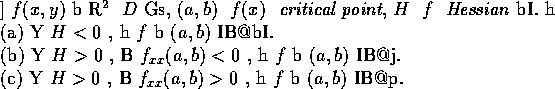
注意. 在本定理中若 H>0, 則因
fxx(a,b)fyy(a,b)=H+fxy(a,b)2>0,
故
fxx(a,b) 和
fyy(a,b) 同號, 因此在 (b), (c) 二款中,
可以用
fyy(a, b) 代替
fxx(a,b) 而定理的結果不變.
這定理的完整證明要用到將在下冊討論的多變數函數的 Taylor 定理.
此處我們仍然利用把變數限制到每個方向的技巧, 看能夠得到多少結果.
若 (a,b) 是 f 的臨界點, 則對任何單位向量
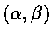 ,
函數
,
函數
均在 t=0 有一臨界點. 再假設 f 有連續二階偏導函數,
則由 chain rule 知
式中
A=fxx(a,b) ,
B=fxy(a,b) ,
C=fyy(a,b).
若 H(a,b)<0, 即
B2-AC>0, 則可找到
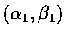 ,
使沿此向量有 g''(0)>0,
也可以找到
,
使沿此向量有 g''(0)>0,
也可以找到
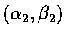 使沿此向量有
g''(0)<0. 故把 f 限制在
使沿此向量有
g''(0)<0. 故把 f 限制在
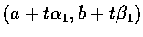 方向,
則 (a, b) 為一真正的谷點.
把 f 限制在
方向,
則 (a, b) 為一真正的谷點.
把 f 限制在
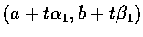 方向,
則 (a, b) 為一真正的峰點. 這便是說 (a,b) 是 f 的鞍點.
(a)的情形遂得證.
方向,
則 (a, b) 為一真正的峰點. 這便是說 (a,b) 是 f 的鞍點.
(a)的情形遂得證.
若 H(a,b)>0, 則用上面的方法可知把 f 限制到過 (a,b)
的任何方向
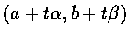 所得函數 g 都在 t=0,
即 (a,b) 處, 有極大(
fxx(a,b)<0 時), 或極小 (
fxx(a,b)>0 時).
可惜, 限制到個方向都有極大, 並不保證原來函數在該處有極大,
極小情形也一樣 (見下面例 16). 所以用這種討論的方式不能證明 (b) 和 (c).
所得函數 g 都在 t=0,
即 (a,b) 處, 有極大(
fxx(a,b)<0 時), 或極小 (
fxx(a,b)>0 時).
可惜, 限制到個方向都有極大, 並不保證原來函數在該處有極大,
極小情形也一樣 (見下面例 16). 所以用這種討論的方式不能證明 (b) 和 (c).
讓我們再舉一些例子:
例 12
令
f(
x,
y)=
x3+
y3-3
xy. 則
故方程式
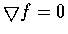
有兩組解: (0,0) 和 (1,1). 又因
故
f 的 Hessian = 36
xy-9. 在 (0,0) 處
Hessian = -9, 故此處
f 有一鞍點. 在 (1,1) 處 Hessian= 27,
而
f(1,1)=6, 故
f 在此處取得極小值
f(1,1)=-1.
例 13
求
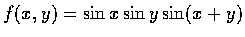
在
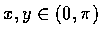
時的極值.
解.
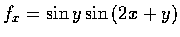 ,
,
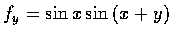 .
因
.
因
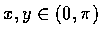 ,
故
,
故
解得臨界點為
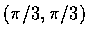 及
及
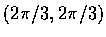 .
又
.
又
故
因此得
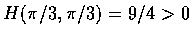 ,
,
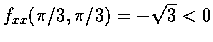 .
遂知 f 在
.
遂知 f 在
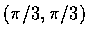 處取得極大值
處取得極大值
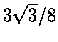 .
又
.
又
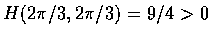 ,
,
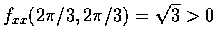 .
遂知 f 在
.
遂知 f 在
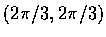 取得極小值
取得極小值
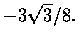
解. 設 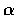 為正實數, 考慮過原點的拋物線
為正實數, 考慮過原點的拋物線



Next: Extrema with constraints
Up: 多變數函數的微分學
Previous: Higher Order Derivatives
1999-06-28
![]() ,
f 為定義在 D 中實數值函數,
a 為 D 的內點. 若有一正數 r 存在, 使當
| x-a | <r 時恆有
,
f 為定義在 D 中實數值函數,
a 為 D 的內點. 若有一正數 r 存在, 使當
| x-a | <r 時恆有
![]() ,
則稱 f 在 x=a 處取得相對 (或局部) 極大值 (relative
or local maximum) f(a). 若將以上討論中的
,
則稱 f 在 x=a 處取得相對 (或局部) 極大值 (relative
or local maximum) f(a). 若將以上討論中的
![]() 符號改為
符號改為 ![]() ,
則稱 f 在 x=a 處取得相對
(或局部) 極小值 (relative or local minimum) f(a).
相對極大值和相對極小值統稱相對 (或局部) 極值 (extremum).
在上下文不發生混淆的時候, 相對 (或局部) 的字樣可以省略.
,
則稱 f 在 x=a 處取得相對
(或局部) 極小值 (relative or local minimum) f(a).
相對極大值和相對極小值統稱相對 (或局部) 極值 (extremum).
在上下文不發生混淆的時候, 相對 (或局部) 的字樣可以省略.
![]()
![]() .
設 i 為正整數,
.
設 i 為正整數,
![]() ,
考慮單變數 t 的函數
,
考慮單變數 t 的函數
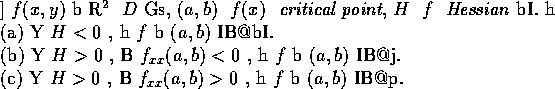
![]() ,
函數
,
函數
![]() 所得函數 g 都在 t=0,
即 (a,b) 處, 有極大(
fxx(a,b)<0 時), 或極小 (
fxx(a,b)>0 時).
可惜, 限制到個方向都有極大, 並不保證原來函數在該處有極大,
極小情形也一樣 (見下面例 16). 所以用這種討論的方式不能證明 (b) 和 (c).
所得函數 g 都在 t=0,
即 (a,b) 處, 有極大(
fxx(a,b)<0 時), 或極小 (
fxx(a,b)>0 時).
可惜, 限制到個方向都有極大, 並不保證原來函數在該處有極大,
極小情形也一樣 (見下面例 16). 所以用這種討論的方式不能證明 (b) 和 (c).
![]() ,
,
![]() .
因
.
因
![]() ,
故
,
故
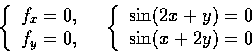
![]() 為正實數, 考慮過原點的拋物線
為正實數, 考慮過原點的拋物線