


Next: About this document ...
Up: 多變數函數的微分學
Previous: 極大和極小
例 15
A cylindrical can contains
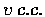
of juice. Find the radius of its two ends and its height so
that it is constructed with the least amount of material.
Solution. Let the radius of either end be x cm. and
the height be y cm. respectively.
Then the surface area
is
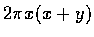 and the volume is
and the volume is
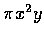 .
We want to
minimize the surface area subject to the condition that the volume is the
constant
.
We want to
minimize the surface area subject to the condition that the volume is the
constant 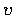 .
This leads us to consider the critical values of the function
.
This leads us to consider the critical values of the function
Equating the partial derivatives of 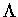 with respect to x, y
and
with respect to x, y
and 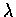 to 0, we get
to 0, we get
From (3) we see that 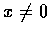 .
Hence (2) implies that
.
Hence (2) implies that
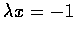 .
Substituting into (1), we get 2x+y-2y=0, or y=2x.
This, together with (3), gives
.
Substituting into (1), we get 2x+y-2y=0, or y=2x.
This, together with (3), gives
例 16
Find the maximum of the product of n non-negative
numbers when their arithmetic mean is given.
Solution. Let the n non-negative numbers be
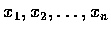 and let their arithmetic mean be a.
Our task is to maximize the function
and let their arithmetic mean be a.
Our task is to maximize the function
under the constrait
Consider the function
To evaluate its critical values,
solve the following equations which are obtained by
equating its partial derivatives to 0.
Multiply the n equations in (5) together, and we obtain
As the maximum will not occur where one of the xi is 0,
it is legal to divide (6) with each of the equations in (5),
and we obtain
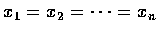 .
Substituting into the constraint,
we get that the common value of the xi is a.
This result may be formulated as the following theorem:
.
Substituting into the constraint,
we get that the common value of the xi is a.
This result may be formulated as the following theorem:
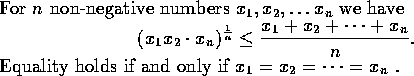
Strictly speaking, as a complete proof of this fact, the above discussion
contains a gap, because we do not know whether the critial point yields
a maximum, a minimum or a saddle point. Though this gap may be mended
by some compactness argument, it lies beyond the scope of the present
course. For general educational purpose, we present below an algebraic
proof of Theorem 9:
Proof (Cauchy). The case n = 2 is done in the following way:
with wquality valid for
x1=x2 .
Assume that we have the result for n=2k , and let 2k+1
non-negative numbers
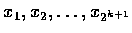 be given.
Then
be given.
Then
習

題
- 1.
- 若
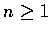 ,
,
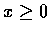 ,
,
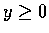 ,
證明
,
證明
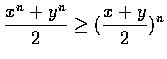 .
.
提示. 在 x+y= 常數的條件下求函數
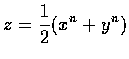 的極小值.
的極小值.
- 2.
- Let
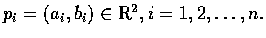 Find the point
Find the point
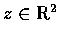 where
where
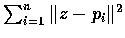 achieves minimum.
achieves minimum.
- 3.
- 在 ellipsoid
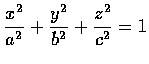 內嵌入有最大體積的直角平行六面體.
內嵌入有最大體積的直角平行六面體.
- 4.
- 設製造貨櫃底的材料每平方公尺價值 1200 元, 其邊每平方公尺為 700 元.
欲使貨櫃容積為 14 立方公尺, 問貨櫃之長, 寬, 高各如何始可使材料費為最小?
- 5.
- 求 (7,-2,3) 到曲面
x2+4y2+z2-20x+16y+16=0 的最短和最長距離.
- 6.
- 在間隔 [1, 3] 中用一次函數 ax + b 來近似地代替函數 x2使得絕對偏差
為最小.
- 7.
- (David A. Smith) 設
f(x, y)=e-y2(2x3-3x2+1)+e-y(2x3-3x2).
(a) 試證 f(x,y) 的唯一的 critical point 在 (0,0),
且 f(0,0)=1 是它的相對極大值.
(b) 驗證
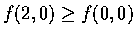 .
.
註. 從本題可以看出:就定義在全平面上的兩個變數的函數而言,
唯一的 critical point 為相對極大值時仍未必是絕對極大值.



Next: About this document ...
Up: 多變數函數的微分學
Previous: 極大和極小
1999-06-28
![]() and the volume is
and the volume is
![]() .
We want to
minimize the surface area subject to the condition that the volume is the
constant
.
We want to
minimize the surface area subject to the condition that the volume is the
constant ![]() .
This leads us to consider the critical values of the function
.
This leads us to consider the critical values of the function
![\begin{displaymath}x =\sqrt[3]{\frac{\upsilon }{2\pi } },
\quad y=\sqrt[3]{\frac{4 \upsilon }{\pi} }
\end{displaymath}](img278.gif)
![]() and let their arithmetic mean be a.
Our task is to maximize the function
and let their arithmetic mean be a.
Our task is to maximize the function
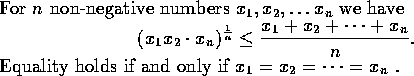
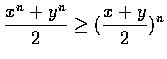 .
.
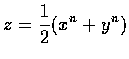 的極小值.
的極小值.
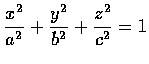 內嵌入有最大體積的直角平行六面體.
內嵌入有最大體積的直角平行六面體.