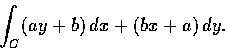Next: About this document ...
Up: 線積分與重積分
Previous: Green 定理
這積分可以視作
e-(x2+y2) 在第一象限 D 上的積分.
利用極座標可將上式改寫為
但顯然 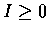 .
開方乃得
.
開方乃得
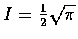 .
.
即令我們接受了用極座標求積分的公式, 上項討論仍有問題.
該公式適用的範圍是有界的區域, 而我們竟把它用到整個的第一象限了.
這就是說對這結果我們仍須作適度的驗證.
為本結果作數值的驗證 (numerical verification) 並不難.
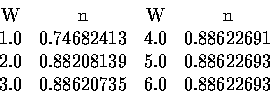
首先注意應得的答案是
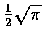 =0.88622693.
然後請同學跑到計算實驗室去, 寫一個程式, 利用 Simpson 法求積分
=0.88622693.
然後請同學跑到計算實驗室去, 寫一個程式, 利用 Simpson 法求積分
之值. 按照上限 U 之不同, 應可以算出以下諸積分值:
以上的計算更加使我們相信
了. 但我們尚須在嚴格的理論基礎上 derive 這結果. 方法如下:
令
則有
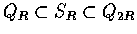 .
令
f(x, y)=e-x2-y2, 則 f(x, y)>0, 故得
.
令
f(x, y)=e-x2-y2, 則 f(x, y)>0, 故得
但
同理
故
從極限的夾擠定理得
但上面的極限等於 I , 我們乃得所要的結果
習

題
- 1.
- 試計算
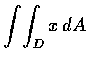 之值, 式中 D 表示界於圓
x2+y2=1 和橢圓
x2+4y2=1 之間的區域..
之值, 式中 D 表示界於圓
x2+y2=1 和橢圓
x2+4y2=1 之間的區域..
- 2.
- 試計算
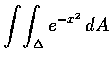 之值.
式中
之值.
式中 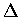 之值為以 (0, 0), (1, 0) 和 (1, 1) 為頂點的三角形.
之值為以 (0, 0), (1, 0) 和 (1, 1) 為頂點的三角形.
- 3.
- 試求由
x=0, z=0, 2x+3y=6, 4x+3y=12 和 2x+y+z=6五個平面所包圍的區域的體積.
- 4.
- Evaluate by Green's theorem the line integeral
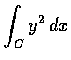 ,
wher C is the rectangle with vertices
(0, 0),
(a, 0), (a, b) and (0, b).
,
wher C is the rectangle with vertices
(0, 0),
(a, 0), (a, b) and (0, b).
- 5.
- Assume that C is a piecewise continuously differentiable
simple closed curve enclosing a domain with area A. Compute



Next: About this document ...
Up: 線積分與重積分
Previous: Green 定理
1999-06-28
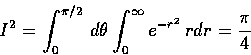
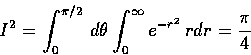
![]() =0.88622693.
然後請同學跑到計算實驗室去, 寫一個程式, 利用 Simpson 法求積分
=0.88622693.
然後請同學跑到計算實驗室去, 寫一個程式, 利用 Simpson 法求積分
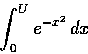
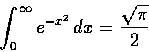
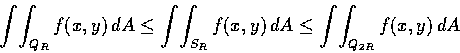
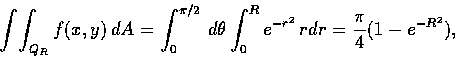
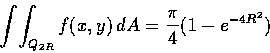
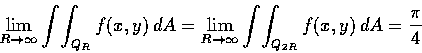
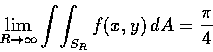
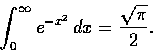
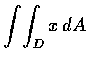 之值, 式中 D 表示界於圓
x2+y2=1 和橢圓
x2+4y2=1 之間的區域..
之值, 式中 D 表示界於圓
x2+y2=1 和橢圓
x2+4y2=1 之間的區域..
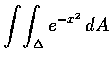 之值.
式中
之值.
式中 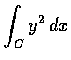 ,
wher C is the rectangle with vertices
(0, 0),
(a, 0), (a, b) and (0, b).
,
wher C is the rectangle with vertices
(0, 0),
(a, 0), (a, b) and (0, b).