


Next: Triple integrals
Up: 面積分與三重積分
Previous: 曲面的表面積
在本節中我們考慮三維空間中的一個固定的 continuously differentiable 曲面
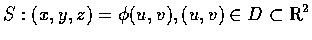 .
在上節的討論中我們引入了向量
.
在上節的討論中我們引入了向量
計算表面積時我們曾利用過這向量的長度. 設
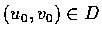 .
則
.
則
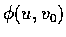 和
和
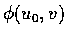 均描寫曲面上的曲線.
均描寫曲面上的曲線.
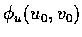 和
和
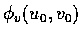 分別是沿這兩條曲線的切線方向的向量.
因此
分別是沿這兩條曲線的切線方向的向量.
因此
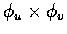 在
(u0, v0) 的值和切平面互相垂直.
它的方向叫作 S 的法線 (normal) 方向. 因此我們得到下列二結果:
在
(u0, v0) 的值和切平面互相垂直.
它的方向叫作 S 的法線 (normal) 方向. 因此我們得到下列二結果:
1) S 在
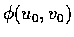 處的切平面方程式為
處的切平面方程式為
這方程式也可以寫成
式中
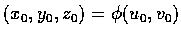 ,
且所有偏導函數的值均在
(u0, v0) 處取得.
,
且所有偏導函數的值均在
(u0, v0) 處取得.
2) 設
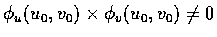 ,
則 S 在
,
則 S 在
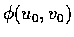 處的法線的參數方程式為
處的法線的參數方程式為
它在該處的單位法向量為
現在介紹面積分的定義. 首先仿照關於曲線長的線積分的觀念,
我們定義在一曲面 S 上的函數
g(x, y, z) 關於 S 的表面積的面積分為
以下舉兩個例子:
例 2
Evaluate
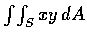
,
where
S is the surface
設 f 為定義於
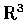 中的區域 D 上的連續可微分的
中的區域 D 上的連續可微分的
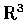 值函數.
我們定義 f 的旋度 (curl) 為
值函數.
我們定義 f 的旋度 (curl) 為
這向量也可以寫成下形:
英國數學家 George Gabriel Stokes (1819--1903) 曾推廣 Green 定理如下:

在本定理的敘述中, 所謂右手螺旋系 (right-hand screw), 純用直觀.
其嚴格的討論和嚴格的證明, 都留給高等微積分.
在 Stokes 定理中取 S 為 xy 平面中的一區域 D. 又設
則有
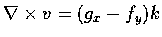 ,
而 xy 平面依右手螺旋系的單位法向量又剛好為 k.
代入 Stokes 定理的公式中, 便得
,
而 xy 平面依右手螺旋系的單位法向量又剛好為 k.
代入 Stokes 定理的公式中, 便得
這便是 Green 定理. 因此 Stokes 定理確是 Green 定理的推廣.
例 3
Let
S be the part of the plane
x+
y+
z=1 in the first octant,
f(
x,
y,
z)=(
f1,
f2,
f3)=(
z2,
x2,
y2) and
C be the boundary curve of
S. Find
Solution. S may be parametrized as
x=u, y=v, z=1-(u+v).
Then
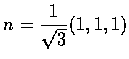 and
and
where 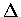 denotes the projection of S on the xy-plane.
In order to compute the line integral
denotes the projection of S on the xy-plane.
In order to compute the line integral
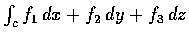 ,
let
C=C1+C2+C3, where
,
let
C=C1+C2+C3, where
and to 0.12truecm
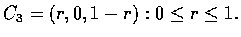
Hence,
Note that this example verifies the Stokes theorem.
習

題
- 1.
- Let
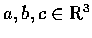 .
Prove that the vector
.
Prove that the vector
is orthogonal to the plane passing through the points a, b and c.
- 2.
- Let f be a twice continuously differentiable function in a domain in
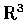 .
Prove that
.
Prove that
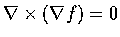 .
.
- 3.
- Let f be a scalar-valued function and v be a vector-valued function defined in a domain D in space.
Assume that they both have continuous parital derivatives in D.
Show that
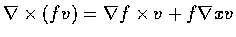 .
.
- 4.
- Compute
where S is the portion of the plane x+y+z=1 lying in the first octant.
- 5.
- Let
f(x, y, z)=(x2, y2, z2), S be the sphere
x2+y2
+z2+1, and n be the unit outward normal from S.
Compute
- 6.
- (a)
- 設 u=9x,
v=3x+2x3+6xy2, w=3z,
f(x, y, z)
=(u, v, w). 求 curl
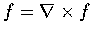 .
.
- (b)
- 設 surface S 為
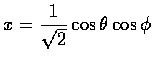 ,
,
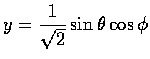 ,
,
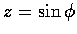 ,
其中
,
其中
![$\theta \in \left[0, 2\pi \right] $](img85.gif) ,
,
![$\displaystyle\phi \in \left[0, \frac{1}{2\pi} \right]$](img86.gif) .
求 S 的單位外向法向量 n (unit normal vector to S).
.
求 S 的單位外向法向量 n (unit normal vector to S).
- (c)
- 設 f 及 S 如 (a), (b) 所述, 試計算面積分 (surface integral)
- 7.
- Compute
where v=xyk, k being the unit vector along the positive z -axis,
and n is the unit outward normal to the surface S of the cube between the planes
x=0, x=1, y=0, y=1, z=0 and z=1.
- 8.
- 設 u=9x,
v=3x+2x3+6xy2, w=3z. S 為 ellipsoid
2x2+2y2+z2=1
之上半, n 為該 ellipsoid 的單位外向法向量. 試直接計算
之值, 並用 Stokes 定理驗證之.
- 9.
- Let T be a solid bounded by a smooth closed surface
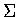 and let n be the unit outward normal vector to
and let n be the unit outward normal vector to 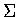 .
Assume that v is a continuously differentiable victor field in a domain containing T.
Prove that
.
Assume that v is a continuously differentiable victor field in a domain containing T.
Prove that
- 10.
- 以 R 和
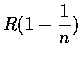 為半徑做兩個同心圓. 從圓心 O 做 m 條射線,
將二圓各分為 m 等分. 設大圓上的分點依次為 p1, p2,
為半徑做兩個同心圓. 從圓心 O 做 m 條射線,
將二圓各分為 m 等分. 設大圓上的分點依次為 p1, p2, 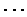 ,
pm 再設 Opk 和小圓的交點為 qk,
,
pm 再設 Opk 和小圓的交點為 qk,
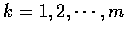 .
令 l(m, n) 為折線
.
令 l(m, n) 為折線
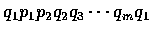 的長.
試計算
的長.
試計算
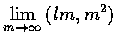 ,
,
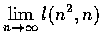 及
及
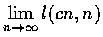 之值,
式中 c>0.
之值,
式中 c>0.



Next: Triple integrals
Up: 面積分與三重積分
Previous: 曲面的表面積
1999-06-28
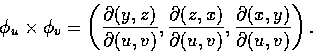
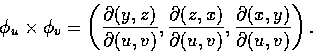
![]() 處的切平面方程式為
處的切平面方程式為
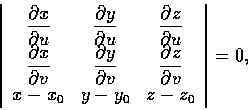
![]() ,
則 S 在
,
則 S 在
![]() 處的法線的參數方程式為
處的法線的參數方程式為
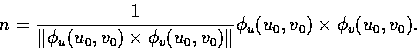
![\begin{eqnarray*}\lefteqn{\int\!\int_S g(x, y, z)\, dA=\int\!\int_D g(\phi (u, v...
...\left[\frac{\partial(x, y)}{\partial(u, v)}\right]^2}\, du\, dv.
\end{eqnarray*}](img56.gif)
![]() 中的區域 D 上的連續可微分的
中的區域 D 上的連續可微分的
![]() 值函數.
我們定義 f 的旋度 (curl) 為
值函數.
我們定義 f 的旋度 (curl) 為
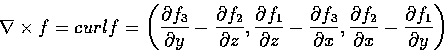
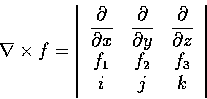

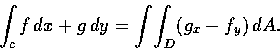
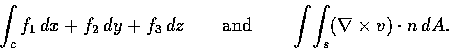
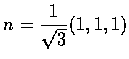 and
and
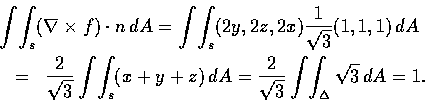
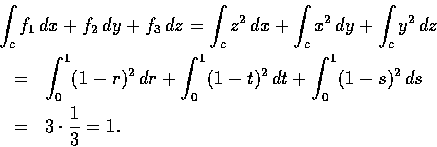
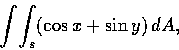
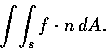
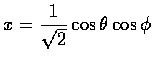 ,
,
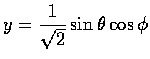 ,
,
![$\displaystyle\phi \in \left[0, \frac{1}{2\pi} \right]$](img86.gif) .
求 S 的單位外向法向量 n (unit normal vector to S).
.
求 S 的單位外向法向量 n (unit normal vector to S).
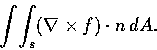
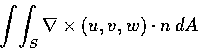
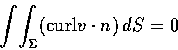
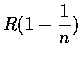 為半徑做兩個同心圓. 從圓心 O 做 m 條射線,
將二圓各分為 m 等分. 設大圓上的分點依次為 p1, p2,
為半徑做兩個同心圓. 從圓心 O 做 m 條射線,
將二圓各分為 m 等分. 設大圓上的分點依次為 p1, p2,