


Next: .
Up: 面積分與三重積分
Previous: 面積分
Since our geometric intuition ends with 3 dimensions,
it is no longer possible to interpret integrals of functions of three or more variables geometrically as areas or volumes.
We can, however, use physical interpretations instead.
Let f(x,y,z) be an everywhere non-negative function defined in a domain D in space.
We may imagine a distribution of mass with density
f(x, y, z) at the point (x,
y, z). Then the total mass in D will be the triple integral (三重積分) of
f(x,
y, z) over D. If
f(x, y, z) also take negative values,
this interpretation breaks down,
since negative density is hard to imagine.
We may instead consider
f[x, y,
z] as a distribution of electric charge per unit volume on a body D made of non-conductive material.
Then its triple integral is the total amount of charge in this body.
This triple integral will be denoted by
We leave the rigorous definetion of the triple integral to a later course,
Ad-vanced Calculus.
Here we only its computation by means of iterated integrals.
Suppose that
以下我們想仿照二維空間的情形討論三重積分的變數變換.
故設 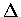 及 D 都是
及 D 都是
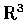 上的有界區域,
上的有界區域,
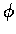 is a one-one mapping from
is a one-one mapping from 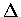 onto D,
且
onto D,
且 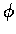 及
及 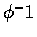 都連續可微.
我們定義行列式
都連續可微.
我們定義行列式
為 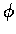 的 Jacobi 行列式 (Jacobian), 通常以
的 Jacobi 行列式 (Jacobian), 通常以
表示. 於是我們有:
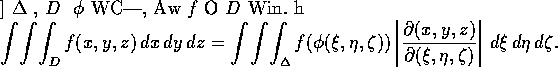
本公式的證明屬於高等微積分的範圍, 姑不詳論.
從直角座標到球座標的變換公式為
此時很容易證明
故有以下的公式:
例 4
我們用球座標再求一次半徑為
R 的球的體積.
因這球內的點的球座標
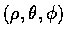
滿足
![$\rho\in[0, R]$](img109.gif)
,
![$\theta\in[0, 2\pi]$](img110.gif)
,
![$\displaystyle\phi\in[-\frac{\pi}{2}, \frac{\pi}{2}]$](img111.gif)
,
故其體積為
In addition to the Stokes theorem,
there is another generalization of the Green theorem to space,
called the Divergence Theorem of Gauss.
This time it involves the triple integral and the surface integral.
For a vector-valued function
f(x, y, z)=(f1(x, y, z), f2(x, y, z), f3(x, y, z))
in a domain D in space,
we define its divergence (散度或散量) as the real-valued function
現在回到 Green 定理. 這定理可以改寫成下形:
設平面區域 D 的邊界 C 為連續可微曲線,
t 為 C 的參數. 令
f=(f1, f2) 為二維向量值函數, 則
式中
為 f 的二維散量, n 為沿
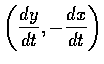 方向的單位向量.
因n和切向量
方向的單位向量.
因n和切向量
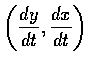 垂直, 故 n 為 unit outward normal vector.
垂直, 故 n 為 unit outward normal vector.
Having this, we may state the Divergence Theorem as follows:




Next: .
Up: 面積分與三重積分
Previous: 面積分
1999-06-28
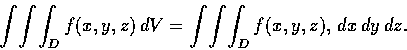
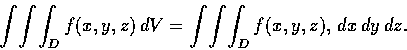
![]() 及 D 都是
及 D 都是
![]() 上的有界區域,
上的有界區域,
![]() is a one-one mapping from
is a one-one mapping from ![]() onto D,
且
onto D,
且 ![]() 及
及 ![]() 都連續可微.
我們定義行列式
都連續可微.
我們定義行列式
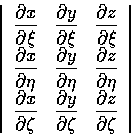
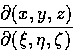
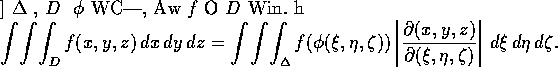
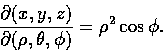
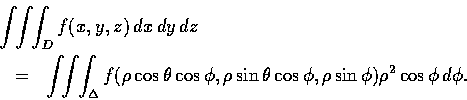
![$\displaystyle\phi\in[-\frac{\pi}{2}, \frac{\pi}{2}]$](img111.gif) ,
故其體積為
,
故其體積為
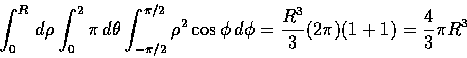
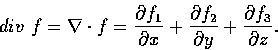
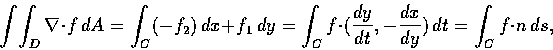
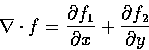
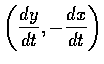 方向的單位向量.
因n和切向量
方向的單位向量.
因n和切向量
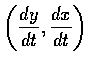 垂直, 故 n 為 unit outward normal vector.
垂直, 故 n 為 unit outward normal vector.
