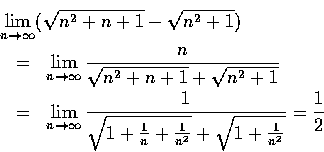Next: 函數的極限
Up: 極限
Previous: 極限
設
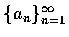 為一數列,
為一數列, 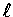 為一實數.
假若``只要 n (即項數) 足夠大,
為一實數.
假若``只要 n (即項數) 足夠大,
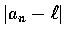 就可任意地小'',
則稱當 n 趨近無限大時, an 趨近於極限
就可任意地小'',
則稱當 n 趨近無限大時, an 趨近於極限 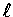 ,
記為
,
記為
為了排版時控制空間, 有時會把
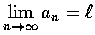 式印成
式印成
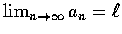 甚至
甚至
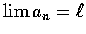 .
請注意, 由定義可知
.
請注意, 由定義可知
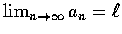 和
和
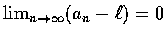 互為充要條件,
也和
互為充要條件,
也和
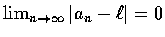 互為充要條件.
互為充要條件.
這是高中理科數學課本所給的極限定義.
它雖然不夠清楚, 但有時也夠用了, 因為在一些簡單的問題中,
我們常可找到適當的常數 K, 使得
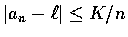 對所有的 n 都成立.
這時真的``只要 n 夠大,
對所有的 n 都成立.
這時真的``只要 n 夠大,
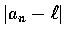 就可以任意地小''了.
就可以任意地小''了.
例 1
試證明
![$\displaystyle\lim_{n\to\infty}\sqrt[n]{\frac13}=1$](img26.gif)
.
證明. 設
![$\theta_n=\sqrt[n]3-1$](img27.gif) .
則
.
則
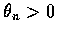 ,
且
,
且
故
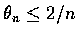 .
於是
.
於是
由此顯然
關於極限的運算有下列公式:
設
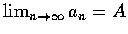 ,
,
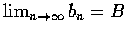 ,
,
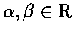 ,
則
,
則
再設 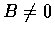 ,
且對一切 n,
,
且對一切 n, 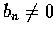 ,
則
,
則
這些公式在高中課本中都曾提過. 在下篇中會給出完整的證明.
利用這些公式常可化簡問題.
例 2
求證
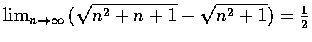
.
證明. 我們有
1999-06-27
![]() 對所有的 n 都成立.
這時真的``只要 n 夠大,
對所有的 n 都成立.
這時真的``只要 n 夠大,
![]() 就可以任意地小''了.
就可以任意地小''了.
![$\displaystyle\lim_{n\to\infty}\sqrt[n]{\frac13}=1$](img26.gif) .
.![]() .
則
.
則
![]() ,
且
,
且
![\begin{displaymath}\left\vert\sqrt[n]{\frac13}-1\right\vert
=\left\vert\frac1{\s...
...t\vert
=\frac{\theta_n}{1+\theta_n}\leq \theta_n \leq \frac2n.
\end{displaymath}](img31.gif)
![\begin{displaymath}\lim_{n\to\infty}\sqrt[n]{\frac13}=1.
\end{displaymath}](img32.gif)
![]() ,
,
![]() ,
,
![]() ,
則
,
則