上面的定義非常含糊. 嚴謹的定義留待下冊. 關於函數的極限也有些運算的公式. 因為高中課本已經詳細討論過這些公式, 也因為它們和數列的極限的運算公式非常相似, 所以我們在此不再重複. 在下編中我們將把這些公式詳細推導出來.
高中課程還提到下面的所謂夾擠定理:
設
![]() ,
且有某 s>0, 使在 0<|x-c|<s 的範圍內
,
且有某 s>0, 使在 0<|x-c|<s 的範圍內
![]() 成立, 則
成立, 則
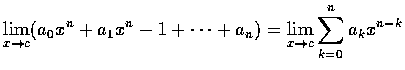
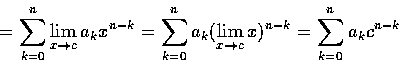
證明. 因
![]() ,
故
,
故
![]() ,
從而
,
從而
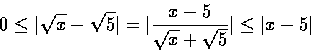
證明. 令
![]() .
則 s>0. 當 |x-c|<s 時,
.
則 s>0. 當 |x-c|<s 時,
![]() 和
和
![]() 同號. 故對
同號. 故對
![]() ,
,
![]() .
在 |x-c|<s 範圍內,
.
在 |x-c|<s 範圍內,
![\begin{displaymath}0\leq \vert \sqrt[m]{x}-\sqrt[m]{c} \vert
=\frac{\vert x-c\ve...
...]{c})^{k-1}}
\leq \frac{(\sqrt[m]{c})^{m-1}}{\vert x-c\vert}.
\end{displaymath}](img68.gif)
註. 上面討論也可用來證明若 n 為正整數, c>0,
則
![]() .
這些事實在習題中要用到. 在這二例中, c=0 時也成立, 只是不能用這種方法證明.
.
這些事實在習題中要用到. 在這二例中, c=0 時也成立, 只是不能用這種方法證明.
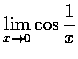 不存在.
不存在.
證明. 我們用歸謬法. 先假設
![]() 存在.
其值為
存在.
其值為 ![]() .
我們希望從這裡導出矛盾. 對
.
我們希望從這裡導出矛盾. 對
![]() 令
令
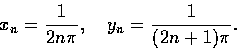
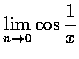 存在而來.
所以
存在而來.
所以
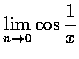 不存在.
不存在.
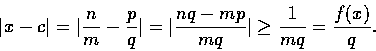
在例 6 中
![]() 不存在.
還有些複雜的例子,
不存在.
還有些複雜的例子,
![]() 存在,
卻不能確知其數值.
另外如例 3、例 5, 則
存在,
卻不能確知其數值.
另外如例 3、例 5, 則
![]() ,
即當 x 趨近 c 時, f(x) 不但有極限, 而且極限值為 f(c).
這種特性通常稱為 f 在 c 點為連續函數 (continuous function).
假若對間隔 I 內的每一點 c,
,
即當 x 趨近 c 時, f(x) 不但有極限, 而且極限值為 f(c).
這種特性通常稱為 f 在 c 點為連續函數 (continuous function).
假若對間隔 I 內的每一點 c,
![]() 都成立,
則稱 f(x) 在 I 上(到處)連續.
在 I 上連續函數的直觀想法是繪製 y=f(x) 的圖形時可以保持筆尖不離紙面.
從例 3 得知多項式函數在實數軸上是到處連續的.
都成立,
則稱 f(x) 在 I 上(到處)連續.
在 I 上連續函數的直觀想法是繪製 y=f(x) 的圖形時可以保持筆尖不離紙面.
從例 3 得知多項式函數在實數軸上是到處連續的.
![$\displaystyle\lim_{n \rightarrow\infty} \sqrt[n]{\frac 15}=1$](img91.gif) ,
(b)
,
(b)
![$\displaystyle \lim_{n \rightarrow 27}\frac{\sqrt{1+\sqrt[3]{x}}-3}{x-27}
=\frac {1}{108}$](img92.gif) .
.
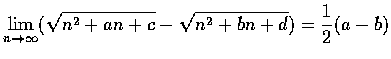 .
.
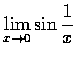 不存在.
不存在.
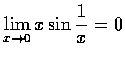 .
.