


Next: 數列的極限
Up: 高中單變數微積分的複習
Previous: 引言
雖然高中數學中建立了複數的體系, 但在微積分中我們只討論實數系.
全部實數的集合我們用
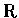 或
或
 表示.
設
表示.
設
 ,
a<b, 我們定義
,
a<b, 我們定義
- 開間隔
-
 ,
a 叫它的左端點
(left end point).
,
a 叫它的左端點
(left end point).
- 開間隔
-
 ,
b 叫它的右端點
(right end point).
,
b 叫它的右端點
(right end point).
- 閉間隔
-
 ,
a 叫它的左端點.
,
a 叫它的左端點.
- 閉間隔
-
![$(-\infty, b]=\{x\in\mathbb{R} : x\leq b\}$](img7.gif) ,
b 叫它的右端點.
,
b 叫它的右端點.
- 開間隔
-
 .
.
- 閉間隔
-
![$[a,b]=\{x\in\mathbb{R} : a\leq x\leq b\}$](img9.gif) .
.
- 半開間隔
-
 .
.
- 半開間隔
-
![$(a,b]=\{x\in\mathbb{R} : a<x\leq b\}$](img11.gif) .
.
在最後的四種間隔中, a 和 b 分別叫它們的左、右端點.
在所有這些間隔裡, 不是端點的點叫它們內點 (interior point).
在閉間隔的定義裡, 我們也允許 a=b,
即 [a,a] 表示只包含 a 一個點的集合  .
這間隔沒有內點.
.
這間隔沒有內點.
我們也有時使用符號  代表``有
代表``有 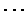 使'',
使'',
 代表``凡
代表``凡 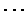 皆''.
皆''.
微積分的全部理論建立在極限 (limit) 的觀念上面.
但必須先有一些直觀的認識, 才容易瞭解極限的嚴謹理論.
以下複習高中課本裡對極限觀念的一些直觀介紹:
1999-06-27
![]() 代表``有
代表``有 ![]() 使'',
使'',
![]() 代表``凡
代表``凡 ![]() 皆''.
皆''.