數學教「識」
三角本事
弦表：三角函數的真諦
感謝《科學月刊》給我 6 頁篇幅，說這一則關於「角」的故事。拋物線的故事說明古希臘數學「並沒有不重實用」，托勒密的弦表則正面表示古希臘也有「超級實用的數學」。弦表不但是最早的函數觀念，也具體呈現了三角函數的真諦 (sin、tan 等)。作者想說的並不是數學史，而是歷史對數學教育的啟發，特別要闡明「角」與「三角」真正應該學習的素養。
科月編輯為這則故事寫的重點摘要非常到位，但我還是想要自我表述這一則故事想要傳遞的重要觀念。
- 本質上「角」的概念始自圓心角；一般三角形的角以及它的典型應用 —
大地測量 — 並非本質，擁有 GPS 與雷射測量工具之後，更顯過時。
- 中國無「角」，這是中、西方數學發展的一個小小分岔，卻造成後來巨大的差異。
- 從歷史的教訓得知：「角」的關鍵作用並非大地測量，而是弧弦互算。
- 三角從一開始就以實用工具的角色出場，西方文化熟悉這個角色，他們的教材也就傾向實用；我國卻固守理論，遇到沒有「公式」的函數（例如 sin 函數）就不知道該教什麼才好，一味追求三角的恆等式與代數性質。
- 我以比較簡明的方式描述了托勒密製作弦表的方法，這種描述可望比較容易在課堂上使用。
我為讀者提供這一篇的全文掃描，並訂正第 46 頁的兩處排版錯誤。但是掃描圖片還是比較難閱讀（解析度無法再高了），推薦大家去找這一期《科學月刊》的紙本來讀（第 657 期，2024 年 9 月），當然最好是能訂閱《科學月刊》！此外，也公佈筆者的原稿如下。
單維彰（2024）九章算術缺少的臨門一「角」：角度、弦表與三角函數的發展。科學月刊，657，42–47。
關於托勒密推導 1 度角之弦長數值（估計值）的方法，在「科普」導向的前文中表達未竟，以下為數學教師同仁勾勒完整的內容。
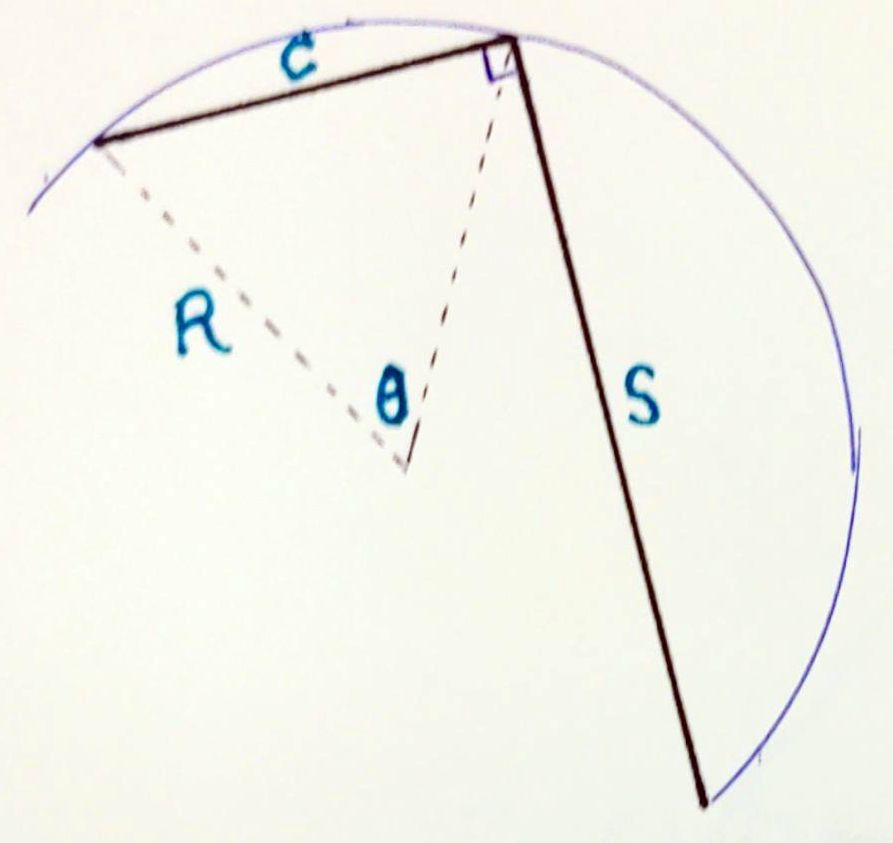首先希望指出：數學老師經常補充的「托勒密四點共圓定理」經常以純數學的面貌登場，用來推論（做證明題），但是它在托勒密心目中的意義卻是計算導向的，用來計算弦長。可以說「四點共圓性質」只是「引理」，托勒密用它來推導真正需要的「定理」，也就是「弦長的差角公式」：
\[\text{crd}(\phi-\theta)={1\over2}\left[\,\text{crd}\,\phi\;\text{srd}\,\theta
-\text{srd}\,\phi\;\text{crd}\,\theta\,\right]\]
公式中 \(\text{srd}\,\theta\) 表示 \(\theta\) 的補弦；
當兩弦與直徑形成直角三角形時，這兩弦互為補弦，如右圖中的 \(c\) 和 \(s\)
兩弦互為補弦。很明顯
\[\text{srd}\,\theta=\text{crd}(180^\circ-\theta)\]
而這裡就是需要引用「四點共圓引理」的地方。令半徑為單位長，則弦與補弦滿足
\[\text{crd}^2\theta+\text{srd}^2\theta=4\]
所以可以從 \(\text{crd}\,\theta\) 算出 \(\text{srd}\,\theta\)。
雖然托勒密時代還沒有負數概念，但他還是另外獲得了弦長的和角公式
\[\text{crd}(\phi+\theta)={1\over2}\left[\,\text{crd}\,\phi\;\text{srd}\,\theta
+\text{srd}\,\phi\;\text{crd}\,\theta\,\right]\]
從而推導弦長的半角公式：
\[\text{crd}\,{\theta\over2}=\sqrt{2-\text{srd}\,\theta}\]
托勒密時代的代數方法不足，他沒有導出弦長的三倍角公式：
\[\text{crd}(3\theta) = 3\,\text{crd}\,\theta - \text{crd}^3\,\theta\]
這條公式還要再等八百年，才會由伊斯蘭文明孕育出來。因此，托勒密不能透過三次方程的數值解來估計弦長。托勒密手中的工具，只能計算和角、差角、半角的弦長。很明顯的出發點是
\(90^\circ\) 和 \(60^\circ\) 的弦長，但是教師可以引導學生試試看：從
\(90^\circ\) 和 \(60^\circ\) 出發，做相加、相減、折半的計算，無法導致
\(3^\circ\)。因此，托勒密需要引用「古典」知識：正五邊形的尺規作圖法。從作圖的程序，托勒密得以推論正五邊形的邊長 —
令正五邊形的外接圓半徑為單位長，則正五邊形的一邊是 \(72^\circ\) 圓心角所對的弦，托勒密算出
\[\text{crd}\,72^\circ={\sqrt{10-2\sqrt5}\over2}\approx1.1755705\]
轉換成三位六十進制小數就是
\[\text{crd}\,72^\circ\approx1\text{ 又 }10\text{ 分 }32\text{ 秒 }3\text{ 忽}
=1.175569\]
（《科月》文章的數據有小錯。）以上「分、秒、忽」分別是六十進制第一、第二、第三位小數的位名，也就是說
\[1\text{ 又 }10\text{ 分 }32\text{ 秒 }3\text{ 忽}=1+{10\over60}
+{32\over3600}+{3\over60^3}\]
然後，托勒密用差角公式獲得
\[\text{crd}\,12^\circ=\text{crd}(72^\circ-60^\circ)\]
的估計值，再用半角公式可以獲得
\[\text{crd}\,6^\circ,\quad\text{crd}\,3^\circ\]
的估計值。
因為沒有弦長的三倍角公式，托勒密無法從 \(\text{crd}\,3^\circ\) 推導
\(\text{crd}\,1^\circ\)。他採取了一個非常「針對性」的方法，這個方法只對這個特定的數值問題有效，而且只對六十進制的三位小數有效（精確到分、秒、忽）。即使沒有所謂的「一般性」，托勒密的方法卻滿足了特定應用問題的需求，成功獲得了數值解。這一段歷史，實在是「數值分析」的典範！
托勒密真可謂「數值分析」的祖師爺。
持續用半角公式，托勒密可以估計以下弦長：
\[\text{crd}\,{3\over2}^\circ,\quad\text{crd}\,{3\over4}^\circ\]
按照「大邊對大角，小邊對小角」的原理，本來 \(1^\circ\) 所對的弦長應該介於
\(\displaystyle{3\over4}^\circ\) 和
\(\displaystyle{3\over2}^\circ\)（也就是
\(\displaystyle1{1\over2}^\circ\)）之間，亦即
\[\text{crd}\,{3\over4}^\circ\leq\text{crd}\,1^\circ
\leq\text{crd}\,{3\over2}^\circ\]
可是托勒密用幾何方法證明了非常「針對性」的夾擠不等式：
\[{2\over3}\,\text{crd}\,{3\over2}^\circ\leq\text{crd}\,1^\circ
\leq{4\over3}\,\text{crd}\,{3\over4}^\circ\]
而且恰好
\[{2\over3}\,\text{crd}\,{3\over2}^\circ
= 1\text{ 分 }2\text{ 秒 }49\text{ 忽 }48\text{ 瞬}\cdots\]
\[{4\over3}\,\text{crd}\,{3\over4}^\circ
= 1\text{ 分 }2\text{ 秒 }49\text{ 忽 }53\text{ 瞬}\cdots\]
以上我暫以「瞬」稱呼六十進制的第四位小數。所以，如果取三位有效的六十進制小數：
\[{2\over3}\,\text{crd}\,{3\over2}^\circ
\doteq {4\over3}\,\text{crd}\,{3\over4}^\circ
\doteq 1\text{ 分 }2\text{ 秒 }50\text{ 忽}\]
這樣就把 \(\text{crd}\,1^\circ\) 準到「忽」位的估計值「夾」出來了：
\[{2\over3}\,\text{crd}\,{3\over2}^\circ \doteq \text{crd}\,1^\circ
\doteq{4\over3}\,\text{crd}\,{3\over4}^\circ\]
注意以上「\(\doteq\)」意思是在三位六十進制小數範圍內相等。於是托勒密獲得以下數值：
\[\text{crd}\,1^\circ\approx 1\text{ 分 }2\text{ 秒 }50\text{ 忽}\]
有了 \(\text{crd}\,1^\circ\) 的估計值之後，托勒密用差角公式獲得
\[\text{crd}\,{1\over2}^\circ=\text{crd}({3\over2}^\circ-1^\circ)\]
的估計值，然後持續用和角、倍角公式推算解析度為
\(\displaystyle{1\over2}^\circ\) 且精確度為「忽」的弦表。
最後補充一個歷史細節：托勒密的弦表用「單位、分、秒」三位有效數字表示弦長，並沒有用「忽」。那是因為他假設半徑為 \(60\) 單位。總之，托勒密算出六十進制三位有效數字的弦表。