Next: 其他代換
Up: 更多代換的例子
Previous: 簡單的三角代換
仿上節
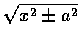 的問題也常可用 hyperbolic functions 代換,
舉例如下:
的問題也常可用 hyperbolic functions 代換,
舉例如下:
例 30
設
a>0, 求
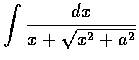
.
解. 令
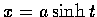 ,
則
,
則
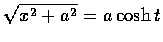 .
.
因
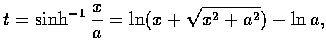
故
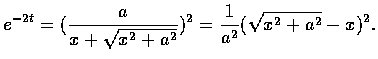
故該積分等於
例 31
求
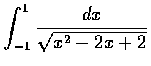
.
解. 設
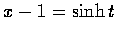 ,
即
,
即
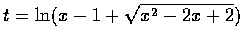 .
則
.
則
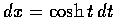 ,
,
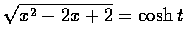 .
.
你如果記得
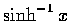 的導函數的公式的話, 本題亦可寫成
的導函數的公式的話, 本題亦可寫成
例 32
求
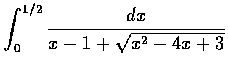
.
解. 因
x2-4x+3=(x-2)2-1, 知當
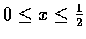 時, 2-x>1.
故可令
時, 2-x>1.
故可令
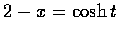 ,
t>0. 於是
,
t>0. 於是
又
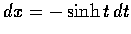 ,
,
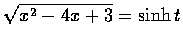 .
故
.
故
1999-06-27
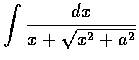 .
.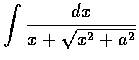 .
.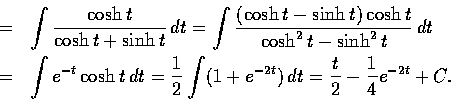
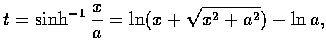
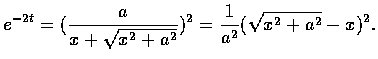
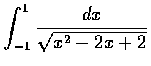 .
.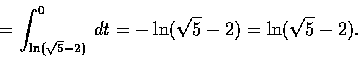
![]() 的導函數的公式的話, 本題亦可寫成
的導函數的公式的話, 本題亦可寫成
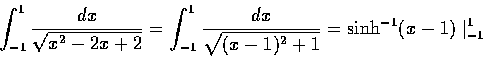
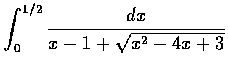 .
.