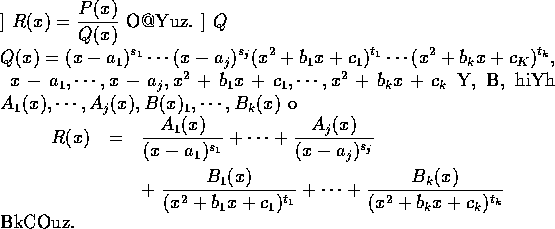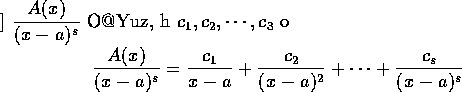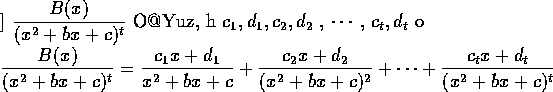Next: .
Up: 微積分講義上篇
Previous: Triple integrals
In our disscussions on the integration of rational functions,
we stated a few theorems on partial fractions.
The aim of this appendix is to prove them.
Our proofs will be base on the Euclidean algorithm (輾轉相除法)
to find the HCF (Highest Common Factor,
最高公因式) of two non-zero polynomials r0(x) and r1(x).
Without loss of generality we may assume that
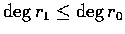 ,
where
,
where 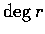 means the degree (次數) of the polynomial r.
The Euclidean algorithm in turn is based upon the division algorithm
(長除法) which provides us with a unique quotient polynomial q1(x)and a remainder polynomial r2(x) such that
means the degree (次數) of the polynomial r.
The Euclidean algorithm in turn is based upon the division algorithm
(長除法) which provides us with a unique quotient polynomial q1(x)and a remainder polynomial r2(x) such that
If r2(x)=0, then it is quite clear that r1(x) is the desired HCF.
Otherwise from (1) it is also clear that the HCF of r1 and r2is the same as the HCF of r0 and r1,
and we may repeat the process to obtain a sequence of polynomials
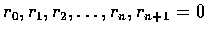 with decreasing degrees such that
with decreasing degrees such that
for some polynomials qk.
The last non-zero polynomial rn is the HCF of r0 and r1.
Lemma 1. Let rn(x) be the HCF of the two non-zero polynomials r0(x) and r1(x).
Then there exist two polynomails a(x) and b(x) such that
證明. We use the notations of the discussions above.
Then from (2), r(x) can be written in the form
rn(x)=A(x)rn-1(x)+B(x)rn-2(x)
with
A(x)=-q(x) and B(x)=1.
Assume that rn(x) can be expressed in the form
Then from (2) we get
rn(x)=[B(x)-A(x)qk-1(x)]rk-1(x)+A(x)rk-2(x),
which is again of the form
rn(x)=A(x)rn-1(x)+B(x)rn-2(x)
with a different A(x) and a different B(x).
Lemma 1 then follows from mathematical induction.
Q. E. D.
Two non-zero polynomials f(x) and g(x) are called relatively prime
(互質) if their HCF is a non-zero constant.
It follows immediately from Lemma 1 that if f(x) and g(x)are relatively prime then there exist polyvomials a(x) and b(x) such that
a(x)f(x)+b(x)g(x)=1.
Lemma 2. Let f(x), g(x) and r(x) be polynomials such that
(a) f(x) and g(x) are relatively prime, and
(b) f(x) is a factor of r(x)g(x),
then f(x) is also a factor of r(x).
證明. From the remarks after Lemma 1 we see the existence of polynomials a(x) and b(x) such that
a(x)f(x)+b(x)g(x)=1.
Hence
r(x)=a(x)r(x)f(x)+b(x)r(x)g(x).
Since f(x) is a factor of both terms on the right,
it is also a factor of r(x). Q. E. D.
Lemma 3. If f(x) and g(x) are relatively prime polynomials,
deg f > 0,
deg g > 0, and if h(x) is another polynomial satisfying
then there exist polynomials r(x) and s(x) such that deg r < deg f,
deg s < deg g,
and
Further the polynomials r(x) and s(x) are uique.
證明. By Lemma 1, there are polynomials a(x) and b(x) such that
a(x)f(x)+b(x)g(x)=1.
Hence

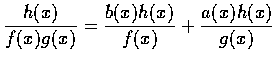 .
to 4truecm
Applying long divisions to the two fractions on the right-hand side,
we get polynomials
q(x), r(x) and s(x) with deg r < deg f and deg s < deg g, such that
.
to 4truecm
Applying long divisions to the two fractions on the right-hand side,
we get polynomials
q(x), r(x) and s(x) with deg r < deg f and deg s < deg g, such that
Clearing up the denominators, we have
h(x)=q(x)f(x)g(x)+r(x)g(x)+s(x)f(x).
If
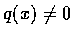 ,
then the degree of the first term on the right-hand side is at least
deg f + deg g, while the degree of every other term in this equation is less than
deg f + deg g. This is impossible. Consequently q(x)=0 and
,
then the degree of the first term on the right-hand side is at least
deg f + deg g, while the degree of every other term in this equation is less than
deg f + deg g. This is impossible. Consequently q(x)=0 and
Next assume that we also have
with deg R < deg f and deg S < deg g. Then
[R(x)-r(x)]g(x)=-[S(x)-s(x)]f(x).
By Lemma 2, f(x) divides
R(x) -r(x). But deg (R-r) < deg f.
Hence R(x)-r(x)=0. Similarly
S(x)-s(x)=0. This proves the uniqueness.
Lemma 4. Let f(x) and g(x) be polynomials,
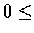 deg f < n deg g, where
n is a positive integer. Then there are polynomials
c1(x),
c2(x) ,
deg f < n deg g, where
n is a positive integer. Then there are polynomials
c1(x),
c2(x) ,
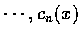 , all of
degrees < deg g, such that
, all of
degrees < deg g, such that
證明. The Lemma is trivial if n=1. Assume that it is true for n-1. Long
division will yield two polynomials q(x) and c(x) such that
f(x)
=q(x)g(x)+cn(x),
where deg q= deg f- deg g<(n-1) deg g and deg c< deg g.
Application of the induction assumption to q(x) and division of both sides by g(x) will produce
Lemma 4 for n.
Now we return to the four basic theorems concerning partial fractions mentioned
in the text:
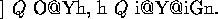
證明. This is but a restatement of the fundamental theorem of algebra,
which can be proved in a course on functions of a complex variables
(複變數函數論).
According to this theorem, Q(x) can be factored into a product of of the form
where c is a real constant and
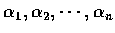 are roots of Q(x). These numbers
are roots of Q(x). These numbers 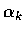 are in general complex numbers and they are not necessarily distinct.
The non-real roots occur in conjugate pairs.
Each real root
are in general complex numbers and they are not necessarily distinct.
The non-real roots occur in conjugate pairs.
Each real root 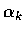 yields a real linear factor,
and each conjuate pair of complex roots yield an irreducible ( 不可約 ) real quadratic factor.
Hence we have this theorem.
yields a real linear factor,
and each conjuate pair of complex roots yield an irreducible ( 不可約 ) real quadratic factor.
Hence we have this theorem.
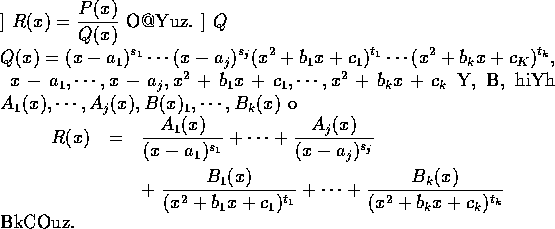
Observe that no two of the linear and quadratic factors have a common root.
Hence they are pairwise relatively prime.
定理5 is thus reduced to a consequence
of Lemma 3.
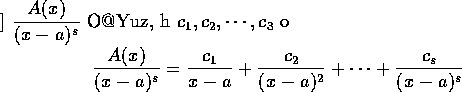
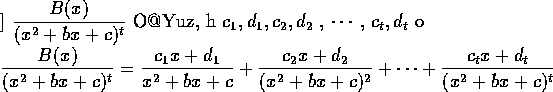
Both theorems follow from Lemma 4 as simple corollaries.



Next: .
Up: 微積分講義上篇
Previous: Triple integrals
1999-06-28
![]() ,
where
,
where ![]() means the degree (次數) of the polynomial r.
The Euclidean algorithm in turn is based upon the division algorithm
(長除法) which provides us with a unique quotient polynomial q1(x)and a remainder polynomial r2(x) such that
means the degree (次數) of the polynomial r.
The Euclidean algorithm in turn is based upon the division algorithm
(長除法) which provides us with a unique quotient polynomial q1(x)and a remainder polynomial r2(x) such that
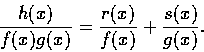
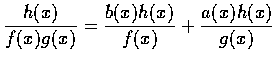 .
to 4truecm
Applying long divisions to the two fractions on the right-hand side,
we get polynomials
q(x), r(x) and s(x) with deg r < deg f and deg s < deg g, such that
.
to 4truecm
Applying long divisions to the two fractions on the right-hand side,
we get polynomials
q(x), r(x) and s(x) with deg r < deg f and deg s < deg g, such that
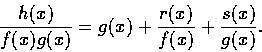
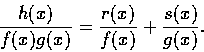
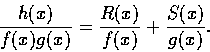
![\begin{displaymath}\frac{f(x)}{[g(x)]^n}=\frac{c_1(x)}{g(x)}+\frac{c_2(x)}{[g(x)]^2}
+ \cdots +\frac{c_n(x)}{[g(x)]^n}.
\end{displaymath}](img135.gif)
![]()